段天璟：等级-规模法则在考古区域分析研究中的相关问题

随着区域性考古调查方法在田野考古实践中的应用，中国考古学界正逐步积累详尽而丰富的数据资料。在此基础上，中外学者引用考古区域分析的方法，在解释聚落形态和社会复杂化进程问题方面进行了有益的尝试。应用相同的方法分析中国考古遗存，不仅有利于世界考古学界进一步了解中国考古遗存所体现的既具有人类社会演进共性又富有鲜明个性的社会发展特点，更有利于我国学者结合本国的研究实际认识、掌握、合理运用并修订相关研究方法。目前所见的区域分析研究中，等级-规模法则(Rank-Size Rule)是在运用调查数据研究社会复杂化问题方面最常用的方法。本文拟讨论该法则的原理、基础并就其在考古区域分析研究中的应用谈谈自己的认识。

一、等级-规模法则的原理

等级-规模法则最早由美国哈佛大学的语言学教授乔治·金斯利·齐普夫(George Kingsley Zipf)推广，是一种经验式的归纳。该法则体现了多样化与统一两种力量之间的竞争。齐普夫用最省力原理解释了这两种力量的互动：多样化力量刺激在原材料产地附近出现大量的“小型的、广泛分布的和高度独裁的社区”；统一的力量则使原材料向少数大型的生产和消费中心集中①。这两种力量的消长，促使某区域的聚落形成单一中心或使其分裂。当两种力量处于平衡状态时，如以某区域的聚落人口数量由多到少的顺序为等级，那么聚落的人口数量与其等级之间会存在一定的分布规律，即如某聚落的等级为r，其人口应为区域中最高等级人口数量的l/r。若以横坐标为等级、纵坐标为人口数量的点表示各个聚落，这些点的分布规律应遵循对数正态分布(Lognormal Distribution)。把这些点标在横、纵坐标轴均经过对数转换(一般为自然对数转换)的二维坐标上，它们的分布规律将呈现为一条直线。

等级-规模法则为考察聚落等级与人口间的关系提供了一个可供对比的理想状态的连续性分布。美国学者理查德·亚当斯(R.E.W.Adams)和理查德·琼斯(Richard C.Jones)用美国各大城市1970年人口数量的例子形象地说明了这个法则。1970年美国最大城市纽约的人口是7896000人，按照等级-规模法则推断，第三大城市洛杉矶的人口应该是7896000/3即2632000人，第十大城市克利夫兰的人口应为7896000/10，即789600人。实际情况是洛杉矶为281000人，克利夫兰为751000人。于是，可以认为美国城市(至少是大城市)基本遵循等级-规模法则。依据该法则，在得到某个区域中第一等级的中心聚落人口数量后，即可在经过对数转换(一般为自然对数转换)的二维坐标的第一象限内生成一条直线线段，表示遵循等级-规模法则的等级和人口数量的预期分布即对数正态分布(图一，a)。其他聚落的实际人口数量可以按照其等级相应地标于坐标系上，形成一些不连续分布的点。这些点连成的曲线与对数正态分布直线相比较，除二线相近之外，通常还会有两类基本情况：凸形线为几个规模相近的大地点和少量小地点的分布(图一，b)，亦被称为多元分布(Plural Distribution)；凹形线为一个最大规模的地点和一群地点的分布(图一，c)，也被称为首要分布(Primate Distribution)。理查德·亚当斯用城市首位度(Primacy Ratio)的概念(即最大聚落人口数/该地区各聚落人口数之和)说明，首要分布中的最大聚落首位度比预期的要大，多元分布中的最大聚落首位度比预期的要小②。

这一法则在考古学中的应用与20世纪30年代在西欧工业化和城市迅速发展的背景下产生的中心地理论(Central Place Theory)有密切关系。中心地理论常应用于经济地理学和人类学中，为研究具有某种功能的聚落及其构成的区域性互动系统提供了相对合理的框架，即中心地理模式(Central Place Model)。

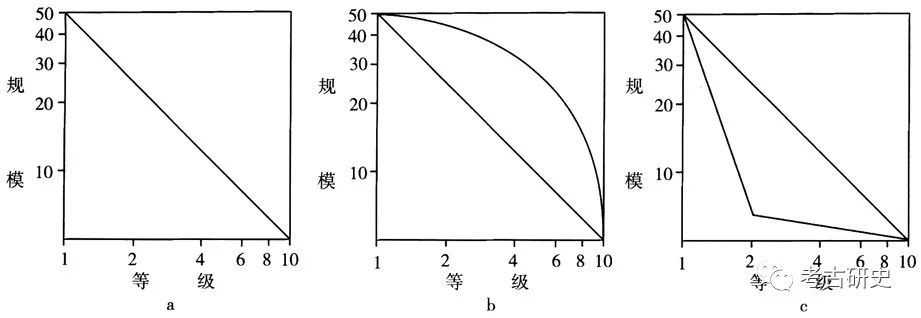
图一 等级-规模分布常见曲线示意图(依Robert D.Drennan and Christian E.Peterson,Comparing Archaeological Settlement Systems with Rank-Size Graphs:A Measure of Shape and Statistical Confidence)

a.预期分布直线 b.凸形线 c.凹形线

当然，典型的中心地理论仅局限于分析经济学中零售商品的生产和销售问题。美国学者乔治·约翰逊(Gregory A.Johnson)通过大量研究认为，忽略市场制度的研究，也可以发现行动的最省力、聚落聚集成群或中心聚落、聚落分级、功能性聚落在空间上的规律性分布等现象，故可以将中心地理论扩展到解释古代聚落形态的研究上③。然而，聚落人口数量的估算与其“功能规模”(Functional Size of a Settlement)间的关系仍是一个存在争议的问题。首先，关于聚落的“功能规模”，美国学者罗伯特·麦考密克·亚当斯(Robert McCormick Adams)④和卡罗尔·史密斯(Carol A.Smith)⑤就由于缺乏精确测量聚落功能规模的有效方法，而对中心地理模式在考古中的应用持怀疑态度。约翰逊也指出，在调查所得的遗址面积中估计聚落的“功能规模”的大小也存在很大难度。其次，虽然西方考古学家通常认为聚落的“功能规模”与人口数量之间直接存在着某种比例关系，但这种比例关系究竟怎样，亦没有一致意见。正如美国学者沙赫特(R.M.Schacht)⑥和阿尔伯特(A.J.Ammerman)⑦等所言，在某一等级各聚落中人口的密度存在着系统多样性。因此，约翰逊认为，尽管一些个案研究显示聚落面积与人口数量间存在某种直线性关系(Linear Relationship)，如成正比关系，但很难断定这种比例关系是一个常数。实际上，聚落面积与人口数量间甚至还会存在某种曲线性关系(Curvilinear Relationship)，如成反比关系，人口数量随聚落面积的增加而减少。

可见，中心地理论在考古学上的应用为我们使用等级-规模法则提供了理论基础，但在考古实践中要特别注意，调查所得的遗址面积与聚落的“功能规模”间，不同形态聚落的“功能规模”与其表征的人口数量间存在着怎样的对应关系。

二、规模和地域的认定：等级-规模法则分析的基础及其问题

目前尚不能确切计算某遗址人口数量的方法，在实践中也无法直接用人口数量来判定某遗址所代表的聚落等级。另外，学者们采用不同的指标，如以“功能规模”来代表人口数量以表示遗址规模。应该注意的是，等级-规模法则是用来衡量某一区域内聚落分布情况的。在考古学研究中，这一区域的界定与考察聚落群的人文地理、政治、经济等特征具有重要关系，也直接影响到研究结果的准确性。可以说，对聚落规模和聚落群分布地域的认定，是等级-规模法则分析的重要基础。

从西方学者在中美洲的玛雅低地、近东地区的美索不达米亚等地的研究中可以看到，一方面，合理选择衡量聚落规模的指标并确定符合实际情况的研究地域，可以使分析结论更加贴近历史的真实；另一方面，由于考古遗存本身的局限性，根据调查得到的遗址数量、面积等与历史上的实际情况相比也存在不同程度的偏差。

亚当斯等人在研究中美洲玛雅古典时期玛雅低地遗址的城市化问题时发现，这个时期的大小建筑均朝向某个庭院(或广场)。各类建筑聚集成的具有某种形式或功能的群落，可称为“庭院群”。“庭院群”聚集发展为玛雅城市。玛雅城市是分散居住的玛雅人的礼仪功能中心。玛雅人附属于居住地附近的礼仪中心，而礼仪中心也依靠属民的人力、食物和组织机构的支持。因此，玛雅城市的建筑既反映了它们与附属人口的关系，也反映了较大的礼仪中心与附近小中心间的关系。另外，由于大型复合建筑(或其附属的卫城)也是礼仪中心功能的重要组成部分，所以它们都成为衡量聚落规模和等级的指标。大型复合建筑的体积一般是庭院的二分之一。于是，礼仪中心即城市规模的计算方法是，大型复合建筑数的二倍加上庭院群的数量⑧。

亚当斯等人的目的是要考察哪些区域的礼仪中心的分布形式更发达。所谓发达的分布形式是指某区域的礼仪中心在地理上既不很聚集又不很分散，其等级-规模分布接近对数正态分布。在地域的界定上，他发现，在玛雅低地选择的蒂卡尔(Tikal)、卡拉克穆尔(Calakuml)、里奥贝克(Rio Bee)、切尼斯(Chenes)四个地理区域中，前二者与后二者的建筑和陶器风格迥异，根据考古学文化特征可以认为分属不同的区域。蒂卡尔与卡拉克穆尔两地的大型礼仪中心间相距50多公里，且各自的聚落呈现出较强的独立性。里奥贝克和切尼斯两地间的间隔更明显，90余公里宽的热带灌木稀树草原阻隔于两地之间。这样，按照考古学文化和地理特征大致划出了四个区域的范围。为了更精确地界定各个区域包含的礼仪中心，亚当斯依据地域毗邻标准在各地区剔除了部分可能属于四地以外其他地区的“边缘”礼仪中心。他认为古典玛雅时期在玛雅低地一天之内步行最远可达35公里⑨。如果某礼仪中心距离本地区最近的较大中心的距离超过35公里，则该中心将被剔除。这样，便精确地界定出了四个考察区域的具体范围。

玛雅古典时期遗存由于庭院等功能区域明显，且多见石构建筑等特征使研究者可以大致估计出其“功能规模”。实际上，由于考古遗存的特殊性质，在很多地区很难从调查得到的遗址面积中具体估计出“功能规模”的大小。于是，不少研究者使用遗址面积代替人口规模进行分析。正如上文指出，遗址的面积与人口间的关系不一定是面积越大人口就越多，故与“功能规模”的方法相比，这种方法存在一定的不确定性。即使假设遗址的面积能够代表人口数量的多少，二者成正比关系，也应当注意，在调查中得到的遗址面积和数量本身就存在一定的“系统错误”。美国学者史蒂芬·福尔克纳(Steven E.Falconer)和史蒂芬·赛维士(Stephen H.Savage)根据美索不达米亚南部和约旦河流域的研究情况指出，首先，调查所得的考古遗址及其代表的人数是一种抽样调查，它们占历史上的实际总量的样本率是不确定的，这个样本率只能通过经验来推断。其次，在调查中确认的遗址数量及其面积的估算也存在着偶然性，特别是一些埋藏较深的多时期堆积遗址或河流冲积地区遗址的面积可能被高估或低估。如有些多时期堆积的遗址往往由于不同时期堆积的影响而使调查所得的面积被高估，相反有些冲击或坍塌地区的遗址可能由于边缘被破坏而被低估了面积。所以该“系统错误”可能丢失或淹没大量遗址尤其是较低等级遗址的数据，对规模-等级分布曲线下段的精度产生较大影响⑩。

综上，遗址的规模和分析地域是等级-规模法则分析的基础。在实践中，用何种数据代表遗址的规模，用怎样的方法界定分析区域，又如何最大限度地避免误差、贴近真实，这些体现着研究者对研究对象的认识程度和研究目的，是分析时应特别注意并重点考虑的问题。

三、形态观察与量化指标：等级-规模法则分析和解读的方法

运用等级-规模法则进行地域分析的主要目的是通过实测数据曲线与预期直线的比较推测分析区域内聚落的社会复杂化程度。

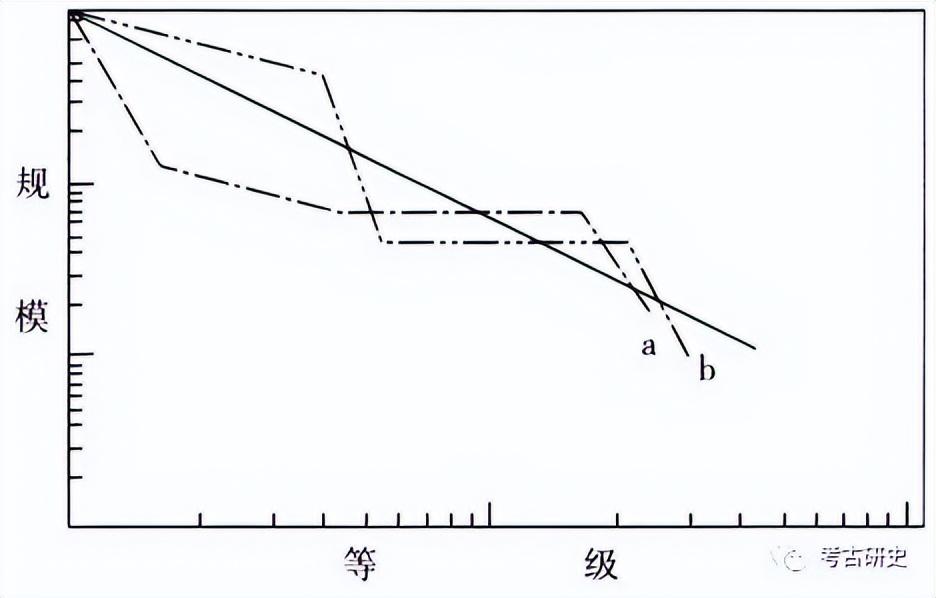
图二 等级-规模分布其他曲线示意图(依Stephen H.Savage,Assessing Departures from Log-Normality in the Rank-Size Rule)

a.延迟凸形线 b.双凸形线

从曲线形态来看，除前述两种基本线形外，实践中还发现有延迟凸形线(图二，a)、双凸形线(图二，b)等。约翰逊、刘莉等认为，当等级-规模曲线呈对数常态直线时，相应聚落的社会发展相当于国家水平(11)。赛维士总结了部分西方学者对各类线形所表征情况的推断。例如，关于首要分布曲线(凹形线)，有意见认为表现了政治、经济发展较简单或城市化的历史较短，或可能将廉价的劳动力集中到了最高等级的聚落；有的认为代表了典型的中心聚落或正在扩张的聚落群；有的认为这种分布形式的聚落是殖民帝国的前身；也有的认为它表现了高度有序的礼仪、大区域内珍贵物品的交流、外交以及主要针对中心聚落的战争；还有的认为这类曲线的形成是聚落群的边界被低估或是仅凭聚落群里部分聚落的数据推测出的结果。关于多元分布曲线(凸形线)，有人认为体现了整合程度较低的聚落系统，或集中了不止一个的聚落系统；也有的认为其中可能包含一个首要分布系统；还有的认为它表现了处于聚落系统外围聚落的分布情况。关于延迟凸形线，表示两个不同的聚落系统同时存在于一个地区，一个首要分布系统叠加在另一个较松散的多元分布系统上；双凸形线，表示多个聚落系统活动于同一区域(12)。

看来，仅根据等级-规模曲线的线形对聚落情况做出的判断存在多种可能。加之上文提到的聚落规模和考察地域的问题，于是利用怎样的方法进行等级-规模分析，怎样在形态观察的基础上进一步解读等级-规模曲线，便成了决定分析结论的关键。

实际上，仅依靠评估曲线形状对分析结果进行解释的方法，回避了等级-规模分布曲线偏离对数正态分布直线多远才能解释为首要分布或多元分布的问题。针对这个问题，美国学者佩因特(R.W.Paynter)等人尝试使用统计学上的K-检验(Kolmogorov-Smirnov test)来检验实测的等级-规模曲线与预期直线间是否存在显著差别(13)。K-检验的原假设是样本来自于与指定的理论分布无显著差异的总体。当K-检验应用于等级-规模检验时，它计算实测规模的累积分布与预期值间的最大差异(14)。将这个最大差异值与据某个特定a值在统计表中查得的预先确定值相比较，如果差异值超出了预先确定值的范围，那就说明实测值与预期值间存在显著差异(15)。

福尔克纳和赛维士指出，在等级-规模分析中，预期值的独立性、分布规律、不连续性以及观测值的抽取方式等四个方面与K-检验的要求存在较大差异。同时，考虑到上文指出的调查所得数据的“系统错误”，他们认为，尽管K-检验的结果仍然可以接受，但要从经验出发对调查数据的可信度进行恰当的估计。考虑到K-检验的局限性，赛维士针对上述调查数据在规模、数量及其取样等方面的特点，使用计算机蒙特卡罗模拟程序(Monte Carlo)(16)的方法进行等级-规模分析。这种方法以某时期调查所得的遗址规模数据占实际存在过遗址的比例(即样本率)的估计值为基础，先计算出实测值与预期值间的K-检验结果以备比较，然后根据最大遗址规模和等级-规模法则创建一个模拟人口区域。模拟人口所在的遗址数量用调查遗址数/估计样本率求得，例如调查得到100个遗址，估计样本率为90%，那么模拟遗址数为100/0.9，即111个。这111个遗址中，最大遗址的规模为调查所得的最大遗址。根据等级-规模法则分布规律模拟出其余110个遗址的规模。之后，计算机将进行多次随机运算(一般为1000次或2000次)，每次从模拟的遗址中随机取出一组与实测遗址数量相等的遗址进行K-检验，得出一系列的检验结果。最后，把最初的实测K值与模拟值相比，计算多少模拟值大于或等于实测值。例如，如果仅3%的模拟值K值大于或等于实测K值，那么实测值显然不是来自等级-规模成对数正态分布的区域。可见，实测K值与模拟值相似的可能性越小，实际的聚落形态的分布情况与对数正态分布的差别就越大。当然，这个方法的精确度与估计的样本率是否准确密切相关。但是，该方法要求分析者通过估计样本率明确地考虑调查取样中存在的问题。进一步讲，遗址的实测值被错误估计的潜在因素，会通过模拟分布中按照预先估定的范围随机增大或减小的遗址规模来表现。例如，为了减小实际观测中可能遗漏更多的小遗址，可以尽可能客观地估计出一个包括从最大城市到小村落的“可浮动”的遗址发现率(如最大城市发现率为95%，而小村落为5%，即95%～5%)。这个概念的引入，能够更严谨地评估实测数据与预期值相似的可能性。福尔克纳和赛维士对美索不达米亚和南黎凡特地区的调查和研究结果显示，在黎凡特沿岸平原早期青铜时代III期，当遗址样本率即可浮动发现率估计为95～5%时，只有整个调查区域的遗址发现率在75%以上时，实测到的分布属于对数正态分布可能性才较低。可见，这种方法强调全面调查和谨慎地考虑遗址的保存及发现情况(17)。

与使用K-检验的方法不同，周南(Robert D.Drennan)和柯睿思(Christian E.Peterson)从等级-规模坐标图出发，引入A系数的概念更加直观地表示实测曲线与预期直线之间的差别(18)。这一系数即为约翰逊所称的等级规模指数(RSI)(19)。周南等人认为，预期直线、经过其与X和Y轴间与坐标轴平行的直线，和坐标系构成了一个矩形，预期直线把这个矩形等分成两个直角三角形。A系数表示实测曲线与预期直线间的面积占其所在的三角形面积的比例。表示实测曲线在预期直线上方的A系数为正数，下方的为负数，当实测曲线与预期直线重合时A为0。A系数为比较不同时期、不同地区聚落的等级-规模曲线与预期直线的差异程度提供了可能。

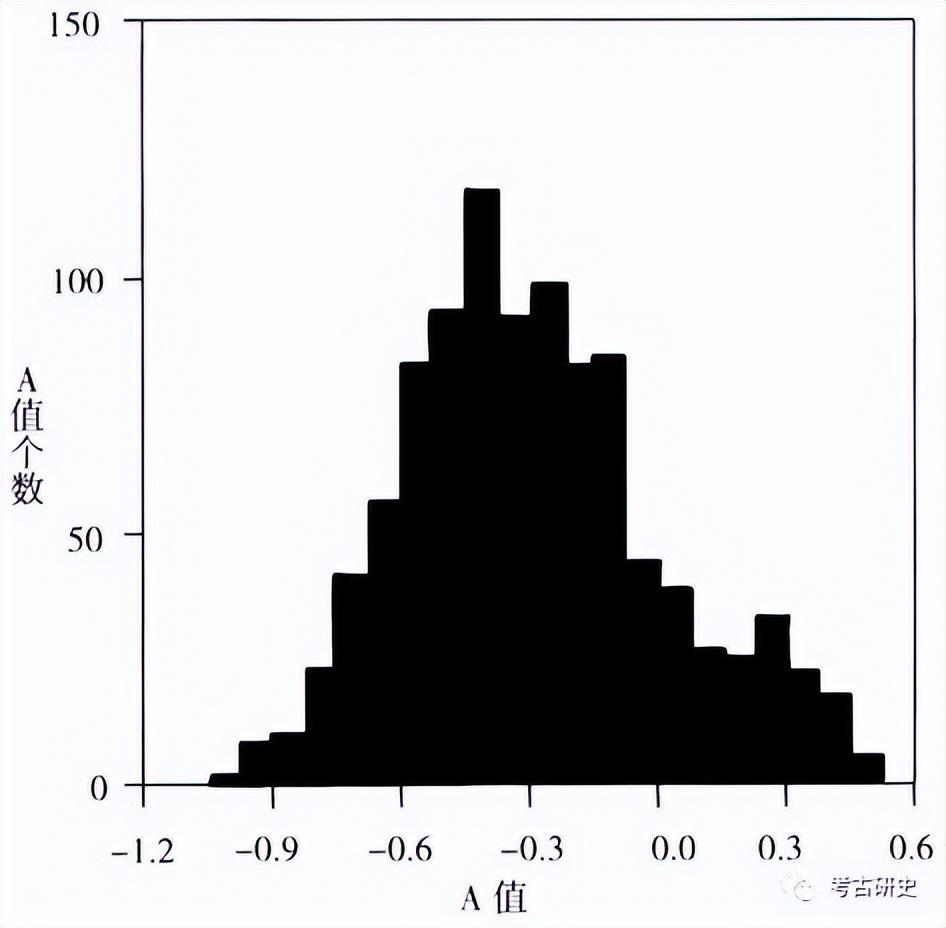
图三 陶寺早期自举A值数据柱状图(依Robert D.Drennan and Christian E.Peterson,Comparing Archaeological Settlement Systems with Rank-Size Graphs:A Measure of Shape and Statistical Confidence)

周南等人还指出，蒙特卡罗模拟方法在实践中不适用于A系数检验差异显著性。在分布有一定数量的固定区域内，使用小于该区域的不同考察范围作1000次蒙特卡罗模拟，得到的平均A值会随考察范围的增大而急剧减小。因为面积越大、包含的大遗址的数量就可能越多，从而影响A值的精确度。于是，考虑到实际工作中经常会出现调查区域无法全面覆盖遗址的实际分布区域的情况，周南等人使用计算机随机自举(Bootstrap)的方法来检验A值和实测曲线的可能分布范围。例如，在分析临汾盆地调查所得的陶寺早期29个遗址面积数据时，便使用1000次随机自举、每次分析29个样本的方法，通过计算每次自举样本的A值获得其误差范围和平均值(图三)。应注意，每次自举过程都应包括最大遗址规模，以保证每个A值代表的曲线与原始观测曲线都开始于同一点。分析时，还要估计自举数据的置信度(Confidence Level)。如置信度为90%，则将自举A值的分布经t分布转换后从小到大100等分，取A值第5～95的数据；如置信度为95%，则取第2.5～97.5的数据。具体转换方法是，将初始的实测A值与1000次自举的平均A值之差，加到1 000个自举分布的每个A值上，从而使自举A值的平均值等于初始A值。这个转换，实际上形成了一个以初始A值为中心的、在一定置信度下的A值及其代表曲线的分布范围。如陶寺早期数据经转换后，在90%的置信度下，A值在-0.957～0.066之间，而预期直线的A值为0。这就意味着，有近90%的把握相信陶寺数据的等级-规模分布与预期分布不同。陶寺早期数据成对数正态分布的显著性水平并不高，可能性(P)仅为0.1多一点。将经转换的自举最大和最小A值所代表的等级-规模曲线标注于坐标上，便成为在90%的置信度下曲线的可能分布范围(图四)。这区域也为我们提供了判断聚落分布动力的可能，如果这个区域紧密地靠近等级-规模曲线，就能够有很大把握相信观测到的遗址分布形式具有较强的动力；若这个区域比较松散地分布于等级-规模曲线的两边，那就说明观测数据不能给我们提供关于这群聚落分布动力的确切情况。

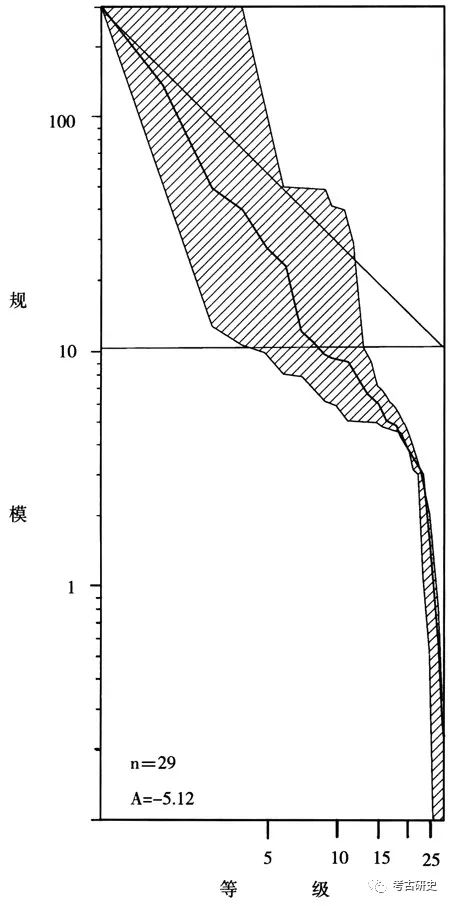
图四 约90%置信度下的陶寺早期聚落等级-规模曲线分布区域图(依Robert D.Drennan and Christian E.Peterson,Comparing Archaeological Settlement Systems with Rank-Size Graphs:A Measure of Shape and Statistical Confidence)

因为A值分析的方法假设的实际人口总数是无穷大，即假设实测到的遗址数是从无穷大的实际遗址数中抽取出来的统计样本，所以周南等人认为，与赛维士等人的K-检验方法相比，A值分析结果与实际情况的接近程度与遗址的发现率无关，而与调查所得的遗址数量有关，遗址数量越多、调查区域越全面，结论就越接近实际。另外，运用A值分析的方法，也可以用来比较某地区不同时期聚落分布的差别，如果某地区不同时期的等级-规模曲线形态差别很大，其A值也会明显不同。例如，在研究伊朗西南部塞琉西亚(Susiana)平原的乌鲁克文化时期(公元前3900～前3200年)的聚落集中化进程时，周南等人按照该地区的编年序列作出了四个时期的等级-规模分布图(图五)。从实测曲线可以看到，这个地区的聚落变化呈凸线形(即多元分布)逐渐减弱的趋势，乌鲁克文化中期实测曲线与预期直线最接近。通过计算出其A值的误差范围可以看到，95%的A值反映了该地区聚落规模分布从苏萨晚期到乌鲁克晚期的变化趋势，但是当置信度在70%左右时，聚落总体上的动态变化情况才开始变得明显起来(图六)。这就意味着，虽然仅有5%的样本可能诱导研究者做出错误结论，但有70%的把握判断塞琉西亚平原乌鲁克文化时期的聚落分布变化呈现出实测曲线所显示的具体变化趋势。周南还指出，实际各个时期用于比较的样本数量越大，反映出的变化趋势就越精确、可信度就越高。同样的道理，A值分析的方法还可以应用于不同地区各个时期间的聚落分布情况的比较。可见，A值分析的方法不仅没有影响依据实测曲线判断聚落分布情况，而且确切地指出，研究者在多大程度上可以信赖等级-规模曲线的分析结果来讨论社会文化变迁。

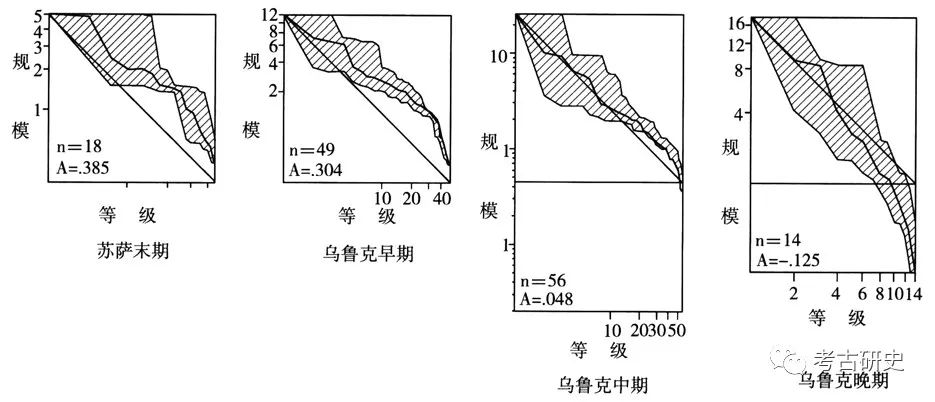
图五 塞琉西亚(Susiana)平原乌鲁克时期90%置信度下聚落等级-规模曲线分布区域图(依Robert D.Drennan and Christian E.Peterson,Comparing Archaeological Settlement Systems with Rank-Size Graphs:A Measure of Shape and Statistical Confidence)

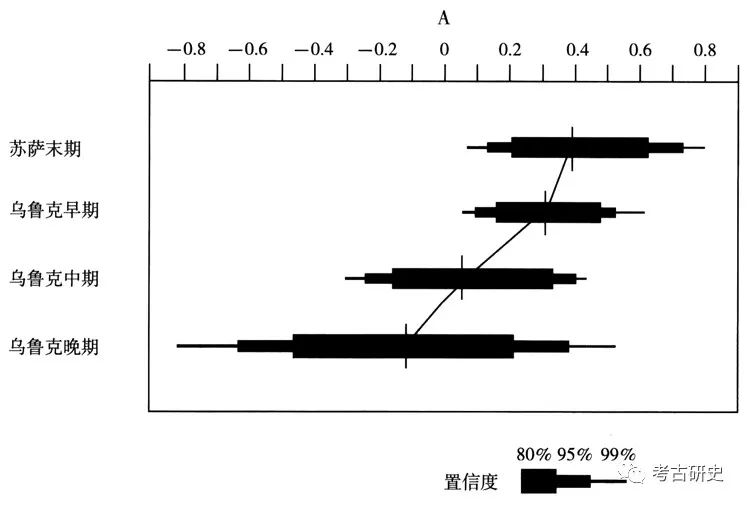
图六 塞琉西亚(Susiana)平原聚落等级规模形态的A值分布图(依Robert D.Drennan and Christian E.Peterson,Comparing Archaeological Settlement System.s with Rank-Size Graphs:A Measure of Shape and Statistical Confidence)

四、关于等级-规模法则在中国应用的简单讨论

自20世纪90年代以来，我国学界引入了系统区域调查的方法，与西方学者联合或独立地开展了区域考古调查工作，如河南洹河流域(20)、伊洛河流域(21)、淮河沿岸(22)，鲁东南沿海地区(23)，内蒙古赤峰地区(24)、岱海地区(25)，成都平原(26)，江西清江盆地(27)等，为学界进一步展开区域性的聚落分析提供了资料，并积累了实践经验。

中国考古学者普遍意识到，遗址规模的判定是直接影响到等级-规模法则分析结果的关键问题，遗址规模判断得越准确，分析结果就越接近真实。与较容易判断规模的中美洲玛雅古典时期的庭院和石构建筑不同，中国多见埋藏于地表之下的包含多个时期堆积的土遗址，且多数遗址仅表现为散布在地面的遗物群(28)，这就增添了判断遗址规模的难度。在实地调查中，中外学者通常采用“拉网式区域调查”的方法，按照每100米距离内3～5片同时期陶片作为界定一个遗址的标准(29)，同时，还采用了考古钻探等方法以弥补地表调查的不足(30)。可以看到，中外学者在抽样调查的前提下，对精准判定遗址规模做出了不懈努力。

同时，中外学者利用中国的材料，运用等级-规模法则进行了分析研究，在分析区域的划分、规模参数的选取方面进行了有益的尝试。

在区域分析研究过程中，分析区域的划分也直接影响着等级-规模法则研究结果的准确性。在上文所述的中外研究中，通常使用较清晰的文化分布和地理范围作为划分分析区域的标准。如刘莉在研究中原地区龙山时代的社会复杂化问题时，就将分析区域分为具有“封闭型聚落群”的陶寺地区(临汾盆地)、豫西地区，具有“半封闭型聚落群”的伊洛河与沁河流域，具有“非封闭型聚落群”的豫北和豫中地区等(31)。这一区域划分方案就与中原地区龙山时代诸考古学文化分布的自然地理区域大体相合。

实际上，我国的区域性考古调查大都在某一自然地理区域内进行，该区域未必与某一文化或某些聚落群体的分布范围重合；某一自然地理区域内也可能存在同一文化的多个类型或不同群体的割据现象。那么，如果不了解这些情况，又应怎样划分区域以便分析呢？

周南(32)、柯睿思(33)在对赤峰地区调查所得数据的分析中，运用在地理信息系统(GIS)中绘制“人口分布地形图”的方法选择规模参数、解决分析区域划分的问题。

在赤峰地区以采集陶片作为判定遗址及其规模的区域调查中，将面积超过1公顷的遗址划分为几个采集点，如果两个采集点的距离超过100米，就把它们分为两个“遗址”来计算面积(34)。柯睿思认为，如果两个采集点的距离仅有50米，那么这两点代表的居址内的人们则可以毫无障碍地进行面对面的日常交流，而1公里以上的间隔则超过了人们能够日常面对面交流的距离，因此距离较近的采集点聚集而成的“遗址”能更好地代表聚落规模。柯睿思等人在绘制“地形图”时，将遗址面积与地表采集陶片的密度换算成“地形图”的“高度值”(z-value)，作为代表遗址所属人口密度的规模(population density)；把“高度值”(z-value)及其所处的位置以100米×100米的方格作为单位，相应地标注在“人口分布地形图”上，可以看到如“地形”般高低起伏的景象(35)。在图上，面积较大、遗存稠密的遗址在图上表现为高峰，反之则为小丘，无遗址发现之处则为平地。周南指出，此图把在空间上邻近的“遗址”自然地群聚在一起，如果选取一条等高线(即某个“高度值”)作为标准，那么“这条等高线常常将几个空间上不相连的遗址归组成一个群聚”(36)。柯睿思和周南通过这种方式，认为赤峰地区红山文化时期共存在65个群聚，除51个小型群体外，在赤峰地区的西北和东南部相对集中地存在14个界定清楚的规模最大的群聚(37)。可以看到，周南等人使用以规模和空间距离为标准的聚类方法，为在区域文化地理界限不明的情况下进行分析提供了可资借鉴的解决方案。

在中国的实践中我们还发现，与西方古典时期的研究不同，由于实际情况未知，在对同一地区、同一文化时期的史前遗址的分析中，可能出现结论不同的情况。如在对赤峰地区西南部半支箭河中游红山时代调查结果的研究中，滕铭予选取遗址面积作为规模参数，运用与周南相同的方法制成了半支箭河中游红山文化时期的“遗址分布地形图”，将遗址分为4个集群。等级-规模分析结果显示，在4个集群中，1群的A值为负值，1群A值接近0，而等级-规模曲线均为“先凸后凹”，其余2群和全部遗址的A值为正值，曲线均为凸线形，故该区域内没有出现地域性中心一级的社会单位(38)。而周南等人的分析则认为，除全部遗址的曲线为正值外，分析的11个聚群的A值有9个为负数，等级-规模曲线呈凹线形，2个的A值为正且接近0，曲线呈直线形；而且，在14个大型聚群中都可以识别出一个最大的单个小型群体。这些都反映出赤峰地区红山文化时期存在中心化了的社会单位。

那么，出现不同结论的原因何在呢？我们发现，二者选取的重点分析区域不同。周南等人重点分析的14个大规模聚群集中分布于赤峰地区的东南和西北部，而滕铭予则主要对赤峰地区西南部的半支箭河中游进行分析。实际上，在周南的分析中，半支箭河中游也没有周南所述的大规模聚群，故二者的结论在整体上看并不矛盾。但这一现象提示我们，对于某一文化而言，选择不同的分析区域可能直接影响到等级-规模分析的结论。

另外，选取不同的聚落规模参数也可能影响分析的结果。如周南等人使用将遗址面积和陶片密度均考虑在内的“人口密度规模”，而滕铭予则直接使用遗址面积作为规模参数。若二者的差别足够大，则势必影响到最后的分析结论。那么，哪类参数更能表现历史上曾存在过的聚落规模呢？目前，学界仍存在不同看法，如张忠培先生就对使用陶片数量求得人口规模的方法表示怀疑，而且认为不能将同一文化的居住址等同为一个聚落(39)。

还应看到，虽然以上两种意见对各自区域内的全部遗址进行分析后都得出了明显的凸线形等级-规模曲线(40)，但是二者从各自的分析结论出发对凸线形曲线进行了不同的解读。周南等人认为，虽然赤峰地区已出现了按照社会等级原则组建起来的社会，但由于此区中存在很多独立的、不属于更高层次中心的社会单位，故在整体分析时出现了凸线形曲线；滕铭予认为凸线形曲线恰好说明了半支箭河中游地区没有地域性中心一级的社会单位。

可见，上述现象正反映出等级-规模法则属于一种“经验式的归纳”的特点。从规模参数和分析区域的选择到等级-规模曲线的解读，均渗透着研究者对古代遗存认识的经验。因此评判哪个结论更接近史实，不仅要看研究者对遗存认识的深度和广度，就上述依据地表调查数据为基础得到的分析结论而言，更有待考古发掘和深入研究来验证。

我们从原理、基础及应用方法的演变等方面撮要介绍了等级-规模法则在考古区域性分析研究中的相关问题。可以看到，等级-规模法则为我们考察古代社会的等级和规模间的关系及其反映的社会形态提供了一个分析的途径。

西方学者意识到了这一方法在实践应用中存在的各种问题，把判读的方法从简单的图形观察改进为量化判断。基于对分析结果误差产生原因的不同理解，产生了运用统计学方法模拟数据范围的K-检验和A值分析等方法。而通过对等级-规模法则在中国区域性分析实践中的考察，我们可以进一步认识和讨论这一方法。

下面，我们就该方法的应用问题简要谈谈自己的看法。

首先，关于等级-规模曲线的含义。约翰逊就曾指出，“我不同意线性分布象征着一个系统的稳定的国家，也不同意非线性的分布就意味着一个变动着的系统。最重要的是，我们应该认为，一个国家系统不能依靠一组属于某段年代序列内单纯的观测(数据)来判断。进一步讲，我们有证据表明某些非线性的分布，如某些首要分布的系统在一个显然是十分稳定的国家内持续了450年”(41)。这也提示我们，考古学实际研究中不能仅根据等级-规模曲线的各类线形就机械地判断其象征着的社会形态。等级-规模曲线勾勒出了聚落分布的形式，只是为我们下一步的社会形态研究提供了线索和佐证。聚落群所代表的社会形态等问题，还得参考其他因素进行综合研究。

其次，关于影响分析结果的因素。我们再来看遗址规模和分析地域这两个等级-功能法则分析的基础。K-检验和A值分析法虽然都是分析实测曲线与预期直线间的差别，但两种方法在设计时，对于影响分析结果因素的理解不同。K-检验认为，分析结果产生误差的原因主要在于调查地域估计不足、遗址面积判断误差等方面。A值分析法则认为分析结果与调查的遗址数量有重要关系，遗址数量越多、调查区域越全面，结论就越接近实际。两种方法都采取了统计学模拟的方法，生成了可资比较的数据。K-检验法，用实测曲线的K值与蒙特卡罗模拟生成的多条曲线的K值相比较，并在模拟时估计了各类样本率以减小误差。A值分析则是通过自举的方法，模拟出了实测曲线在坐标轴上的可能分布范围，其误差的估计是通过A值误差范围的置信度来实现的。

虽然K-检验和A值分析法都努力使分析结果接近真实，但是应该认识到，K-检验和A值分析的结果只对选取的数据负责，而分析结果能否反映历史的真实则与研究者的研究深度、实地调查的精度等有直接关系。

实际上，调查结果的精度、分析区域的划分、规模参数的选取，都会影响到等级-规模曲线的形态及最终的解释。如关于遗址规模的判定，即使承认遗址的面积可以在某种程度上代表遗址的人口规模，但是不同类型和功能的遗址规模怎样换算，如大聚落和小城，哪个优于哪个(42)，这些问题显然是不能够通过改进统计方法来解决的，而需要具体问题具体分析了。

再次，关于考古学文化研究与等级-规模法则的关系。考古学文化研究的深入程度直接决定了对遗址功能的判断、分期方案和分析区域的选取是否恰当。在实际工作中，我们可以考察已发掘的同一文化不同类型的遗址，将遗址形态与出土器物相结合确定各类遗址的功能和规模，为判断调查所得遗址的功能及不同类型遗址规模的换算提供参考。此外，在考古地域分析中对年代的把握也是一个重要问题。考察某地区某时期的聚落分布情况时，应以多长的年代为刻度？这个分期方案的选择直接影响着样本的数量，因为在调查所得遗址数量一定的前提下，分期越细每个时期可用于分析的遗址数量就越少。而分期方案既与聚落实际使用的时间密切相关，又直接关系到研究结果能否恰当反映聚落表征的社会形态的演变。因此，应根据实际情况构建或选择符合研究需要并在工作中易于操作的遗址分期方案。此外，选择分析区域时，既应考虑到自然地理的划分，也要考虑到考古学文化的分布，从而根据研究目的恰当地确定考察区域，使研究结论更加贴近历史的真实。

参考文献：

①George Kingsley Zipf,Human Behavior and the Principle of Least Effort,Cambridge:Harvard University Press,1949,p.352.②R.E.W.Adams and Richard C.Jones,Spatial Patterns and Regional Growth Among Classic Maya Cities,American Antiquity,1981(2),pp.310-311.③Gregory A.Johnson,Aspects of Regional Analysis in Archaeology,Annual Review of Anthropology,1977(6),pp.494-496.④Robert McC.Adams,Anthropological Perspectives in Ancient Trade,Current Anthropology,1974(3),pp.141-160.⑤Carol A.Smith,Economics of Marketing Systems:Models form Economic Geography,Annual Review of Anthropology,1974(3),pp.167-201.⑥R.M.S chacht,Population and Economic Organization in Early Historic Southwest Iran,PhD thesis,Univ.Michigan,1972,p.145.⑦A.J.Ammerman,et al.,Toward the estimation of population growth in Old World prehistory,Univ.New Mexico Press,1976,pp.27-61.⑧R.E.W.Adams and Richard C.Jones,Spatial Patterns and Regional Growth Among Classic Maya Cities,American Antiquity,1981(2),pp.303-310.⑨R.E.W.Adams,Routes of Communication in Mesoamerica:The Northern Guatemala Highlands and the Peten,In Mesoamerican Communication Routes and Cultural Contacts,New World Archaeological Foundation Paper,Provo,1978.⑩Steven E.Falconer and Stephen H.Savage,Heartlands and Hinterlands:Alternative Trajectories of Early Urbanization in Mesopotamia and the Southern Levant,American Antiquity,1995(1),p.42.(11)a.刘莉：《中国新石器时代：迈向早期国家之路》，文物出版社，2007年。b.Gregory A.Johnson,Monitoring Complex System Integration and Boundary Phenomena with Settlement Size Data,Archaeological Approaches to the study of complexity,Institute woor Prea-en Protohistorie,Amsterdam,1981.(12)Stephen H.Savage,Assessing Departures from Log-Normality in the Rank-Size Rule.,Journal of Archaeological Science,1997(24),p.234,Tablel Asummary of the expansions provided for various rank-size outcomes that differ from log-noramlity.(13)R.W.Paynter,Models of Spatial inequality:System Patterns in History Archaeology,Academic Press,New York,1982.(14)S.Shennan,Quantifying Archaeology,Academic Press,New York,1990.(15)D.H.Thomas,Refiguring Anthropology:First Principles of Probability and Statistics,Waveland,Prospect Heights,Illinois,1986,pp.322-337.(16)也称统计模拟方法，是20世纪40年代中期由于科学技术的发展和电子计算机的发明而被提出的以概率统计理论为指导的一类数值计算方法，是使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。该方法通常可分两类：一类是所求解的问题本身具有内在的随机性，借助计算机的运算能力可以直接模拟这种随机的过程；另一种是所求解问题可以转化为某种随机分布的特征数，比如随机事件出现的概率，或者随机变量的期望值。应用蒙特卡罗方法解决实际问题的时候主要有两部分工作：一是模拟某一过程时需要产生各种概率分布的随机变量；二是用统计方法把模型的数字特征估计出来，从而得到实际问题的数值解。(17)Steven E.Falconer and Stephen H.Savage,Heartlands and Hinterlands:Alternative Trajeciories of Early Urbanization in Mesopotamia and the Southern Levant,American Antiquity,1995(1),pp.41-44.(18)Robert D.Drennan and Christian E.Peterson,Comparing Archaeological Settlement Systems with Rank-Size Graphs:A Measure of Shape and Statistical Confidence,Journal of Archaeological Science,2004(31),pp.534-541.本文引用的A值分析的方法和例子，如未特别说明均出自此文。(19)Gorge A.Johnson,The Changing Organization of Uruk Administration on the Susiana Plain,The Archaeology of Western Iran:Settlement and Society from Prehistory to the Islamic Conquest,Smithsonian Institution Press,Washington D.C.Landon,1987,p.109.等级规模系数(Rank Size Index)的计算公式为：

其中N为分析的聚落总数，Pobv为实测聚落规模，Prs为预期直线表示的聚落规模，Pcmax为最大聚落规模。(20)中美洹河流域考古队：《洹河流域考古研究视步报告》，《考古》1998年第10期。(21)a.陈星灿、刘莉、李润权、华翰维、艾琳：《中国文明腹地的社会复杂化进程-伊洛河地区的聚落形态研究》，《考古学报》2003年第2期。b.中国社会科学院考古研究所二里头工作队：《河南洛阳盆地2001-2003年考古调查简报》，《考古》2005年第5期。(22)河南省文物考古研究所、武汉大学考古学系：《河南淮滨县黄土城地区区域考古调查简报》，《华夏考古》2010年第4期。(23)a.中美两城地区联合考古队：《山东日照市两城地区的考古调查》，《考古》1997年第4期。b.中美日照地区联合考古队：《鲁东南沿海地区系统考古调查报告》，文物出版社，2012年。(24)赤峰中美联合考古研究项目组：《内蒙古东部(赤峰)区域考古调查阶段性报告》，科学出版社，2004年。(25)岱海中美联合考古队：《2002年、2004年度岱海地区区域性考古调查的初步报告》，《内蒙古文物考古》2005年第2期。(26)成都平原国际考古调查队：《成都平原区域考古调查(2005-2007)》，见《南方民族考古》第六辑，科学出版社，2010年。(27)江西省文物考古研究所、江西樟树市博物馆：《江西清江盆地区域考古调查简报(2011-2012年度)》，《南方文物》2012年第4期。(28)赤峰中美联合考古研究项目组编：《内蒙古东部(赤峰)区域考古调查阶段性报告》第42页，科学出版社，2004年。(29)同(21)a。(30)同(26)。(3l)刘莉：《中国新石器时代：迈向早期国家之路》第157、161页，文物出版社，2007年。(32)周南、柯睿思：《早期酋长制群体的聚落形态比较研究——以内蒙古东部、安第斯山北部和美洲中部三个地区为例》，《吉林大学社会科学学报》2004年第5期。(33)Christian E.Peterson and Robert D.Drennan,Settlements,Sites and Surveys:Regional-Scale Analysis of Prehistoric Human Interaction,2005(1),pp.5-30.(34)同(25)。(35)Christian E.Peterson and Robert D.Drennan,Settlements,Sites and Surveys:Regional-Scale Analysis of Prehistoric Human Interaction,2005(1),pp.7-10.高度值(z-value)具体算法见该文表5。(36)同(32)。(37)Christian E.Peterson and Robert D.Drennan,Settlements,Sites and Surveys:Regional-Scale Analysis of Prehistoric Human Interaction,2005(1),p.14，图12.(38)滕铭予：《半支箭河中游先秦时期遗址分布的空间考察》，《吉林大学社会科学学报》2009年第4期。(39)张忠培：《内蒙古东部(赤峰)区域考古调查阶段性报告·序一》，《华夏考古》2003年第4期。(40)a.同(32)。b.滕铭予：《半支箭河中游先秦时期遗址分布的空间考察》图5，《吉林大学社会科学学报》2009年第4期。(41)Gregory A.Johnson,Aspects of Regional Analysis in Archaeology,Annual Review of Anthropology,1977(6),pp.497-498.

来源：《考古》2015年第4期