神奇的莫比乌斯带，只有一个曲面可以无限循环

人们都说学无止境，知识是无穷无尽的，总是存在着许多新奇的知识是我们所不了解的。就像莫比乌斯带一样，竟然有着魔术般的神奇性质，能够折成一个曲面，如果放上一只小虫子的话，小虫子可以在上面无限循环的一直爬。下面就一起来看看神奇的莫比乌斯带。

一、神奇的莫比乌斯带

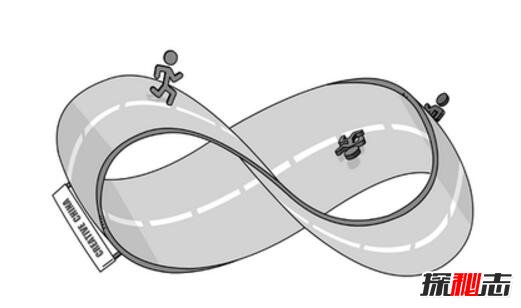
神奇的莫比乌斯带神奇在哪里呢?“莫比乌斯带”是19世纪德国数学家莫比乌斯(Mobius)发现的。在一个阳光美好的午后，莫比乌斯静静的坐在桌前，手中拿着一个长长的纸条，不经意的把纸条拧了一个圈，又把两个头对接了起来。

这时正好有一只小蚂蚁到他的桌面上，他小心翼翼地把小蚂蚁请到了手中的纸上，小蚂蚁也就不停的到处游荡，莫比乌斯轻轻的注视着纸上的小蚂蚁，他发现小蚂蚁虽没翻越任何一处的纸边沿，却爬过了纸表面的每一个地方。这让莫比乌斯非常惊讶。

这就是著名的莫比乌斯带，把一根纸条扭转180°后，两头再粘起来做成的纸带圈，具有魔术般的性质，这种莫比乌斯带只有一个曲面，可以无限的循环往复，与潘洛斯阶梯一样奇妙。

其实莫比乌斯带也是一种拓展图形，它们在图形被弯曲、拉大、缩小或任意的变形下保持不变，只要在变形过程中不使原来不同的点重合为同一个点，又不产生新点。换句话说，这种变换的条件是：在原来图形的点与变换了图形的点之间存在着一一对应的关系，并且邻近的点还是邻近的点，这样的变换叫做拓扑变换，在生活中莫比乌斯带的应用还是挺多的。↓↓↓

二、莫比乌斯带的应用

“莫比乌斯带”在生活和生产中已经有了一些用途。例如，用皮带传送的动力机械的皮带就可以做成“莫比乌斯带”状，这样皮带可以磨损的面积就变大了。

如果把录音机的磁带做成“莫比乌斯带”状，就不存在正反两面的问题了，磁带就只有一个面了。它还能平坦的嵌入三维空间。简易的“莫比乌斯圈”可通过一张长方形纸任何一面反转粘贴。

莫比乌斯带常被认为是无穷大符号「∞」的创意来源，因为如果某个人站在一个巨大的莫比乌斯带的表面上沿着他能看到的“路”一直走下去，他就永远不会停下来。但是这是一个不真实的传闻，因为「∞」的发明比莫比乌斯带还要早。

而且人们在逛地标建筑、买珠宝首饰时只要见到莫比乌斯环式的设计，都会觉得幸运吉祥，甚至会发出“真希望自己的人生是个莫比乌斯环呢”的感叹。遗憾的是懂莫比乌斯环之人，其实少之又少。