123黑洞是什么?数学中的犹如黑洞的存在，结果必是123

导语：123黑洞又被称为西西弗斯串，不管设定什么数字，只要按照规定的法则，结果永远都是固定值123，就像黑洞一样吸住东西就不放手，直到2010年，“123黑洞”现象才被中国回族学者秋屏先生做出了精确的数学证明，但是证明过程及其复杂，下面就跟着探秘志小编一起来看看吧!

123黑洞是什么?

123黑洞就是无论怎么设值，只要在规定的处理法则下，最终都能算出一个相同的固定值，怎么也无法改变，就像宇宙中的黑洞吸住东西就不放手一样，所以就被称为数学中的数字黑洞，简直比世界上最神奇的数字142857还诡异。

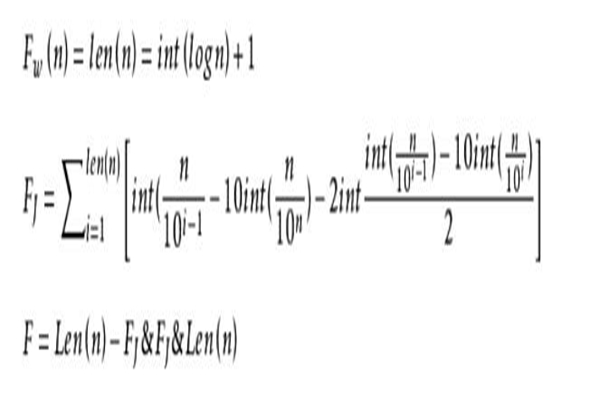
123黑洞又被称为西西弗斯串，任何数值经过运算最终结果都难逃123黑洞。123数字黑洞也可以用几个函数表达它，表达式如图，F是一级函数，k级通项式为它的迭代循环。

123黑洞怎么运算?

任意设定一串数字串，找出其中的奇数个数，偶数个数以及所有数的总数，再按照“偶-奇-总”的顺序排列，可得出一个新数，在不断循环这个算法，其最终结果一定会变成123。

比如1234567890这个数字串，奇数个数为5个，偶数也是5个，总共10个，那么按照“偶-奇-总”的排序，得到新数字5510，再重复以上步骤，5510就得到134,134就得到123，这就印证了任何数也无法逃离最终结果123的黑洞。

为什么会出现123黑洞?

关于123黑洞的具体推演过程十分的复杂，直到2010年，“123黑洞”现象才被中国回族学者秋屏先生做出了精确的数学证明，并推广出六个相似的黑洞：123,213,312,321,132,231，这在秋屏先生的论文《“西西弗斯串(数学黑洞)”现象与其证明》中曾被提到过。

123黑洞现象小编就通过三个例子简要的进行分析：

1. 当设定值是一个个位数时：

如果是奇数，则偶=0奇=1总=1，那么得到011这个新数，偶=1奇=2总=3，这就得到了123。

如果是偶数，则偶=1奇=0总=1，那么得到101这个新数，在推出，偶=1奇=2总=3，也得到123。

2. 当设定值是一个两位数时：

如果是一奇一偶，则偶=1奇=1总=2，得到新数112，有推出偶=1奇=2总=3，则最后得到123。

都是偶数，则偶=2奇=0总=2，新数为202，在推出偶=3奇=0总=3，得出303，再推偶=1奇=2总=3，得到123。

都是奇数，则偶=0奇=2总=2，新数为022，再推偶=3奇=0总=3，再推偶=1奇=2总=3，得到123.

3. 当设定值是一个三位数时：

如果是三个奇数，则偶=0奇=3总=3，得到新数033，在推出偶=1奇=2总=3，又得到了123的结果。

两偶一奇时，则偶=2奇=1总=3，新数213，推出偶=1奇=2总=3，得到123

两奇一偶时，则偶=1奇=2总=3，得到123

由此我们可以推导出：当设定值是一个m(M>3)数时，则这个数由m个数字组成，n个奇数，k个偶数，则m=n k,由knm链接生成一个新数，重复以上步骤，就一定得到一个三位新数knm。

结语：123黑洞的推演看起来复杂，其实仔细想想还是很容易想明白的，数学中还有很多有趣的数字，就比如缺8数，012345679就是没有8，看完你肯定能感受到数学的奇异之处。