算法的形状｜图绘自动写作史（一）：媒介语言中的位值

在当今社会，自动化写作技术及其软件在许多领域变得日益可应用，诸如网络文学、影视剧本创作、新闻媒体等，它同时也伴随着许多伦理与文化争议。也许理解这些争议的出发点，在于思考写作何以变得自动化。写作作为一项古老的文化技艺，在数字与计算机器时代成为了一种数据写入式的、属于机器的简单动作。此外，机器写作愈发变得智能，不仅可以执行读写行为，还可以进行创作。我们如何理解写作机器的创作，它是否是具有创造力的？理解这一美学问题，笔者主张应深入到自动写作的科技文化史当中，不仅分析写作的自动化技术，更应结合自动化技术产生和应用的文化艺术条件，来综合地考量自动写作历史中的重要事件。

历史上关于自动化机器的例子，令我们在对人工智能取代劳动力的焦虑之余，去认识与了解自动写作何以产生、演化的科技文化史中重要的思想实验，也许不失为一种对机器的学习。毕竟，了解机器的操作型媒介与物理过程犹如掌握一门陌异语言。而这种陌异的操作型语言往往在自动写作的演化史中扮演着重要角色，它揭示了技术的发明与应用往往存在于由操作型媒介和语言支撑起的一个个思想实验当中。

本文对于这些思想实验的地图绘制，是对于这些操作型媒介和语言如何激发思想实验和创造的展示。在此意义上，图绘自动写作关心的是美学问题，而美学在这里指的是对于机器与技术的创造力的本体论追问。

思想实验

历史上，自动化指的是工业革命中完全自主自动制造的机械化过程。在战后时代，自动化有着比机械化更加具有系统性和广延性的意味，它指的是制造闭环以控制整个生产流程，包括电子和数字计算机对机械问题的应用。之于写作，自动化写作则是以计算科技为基础的机器写作，包括更具有自动化特征的、以人工智能技术为基础的写作，诸如大众知悉的微软小冰、Replika、ChatGPT等智能机器人、应用和技术。

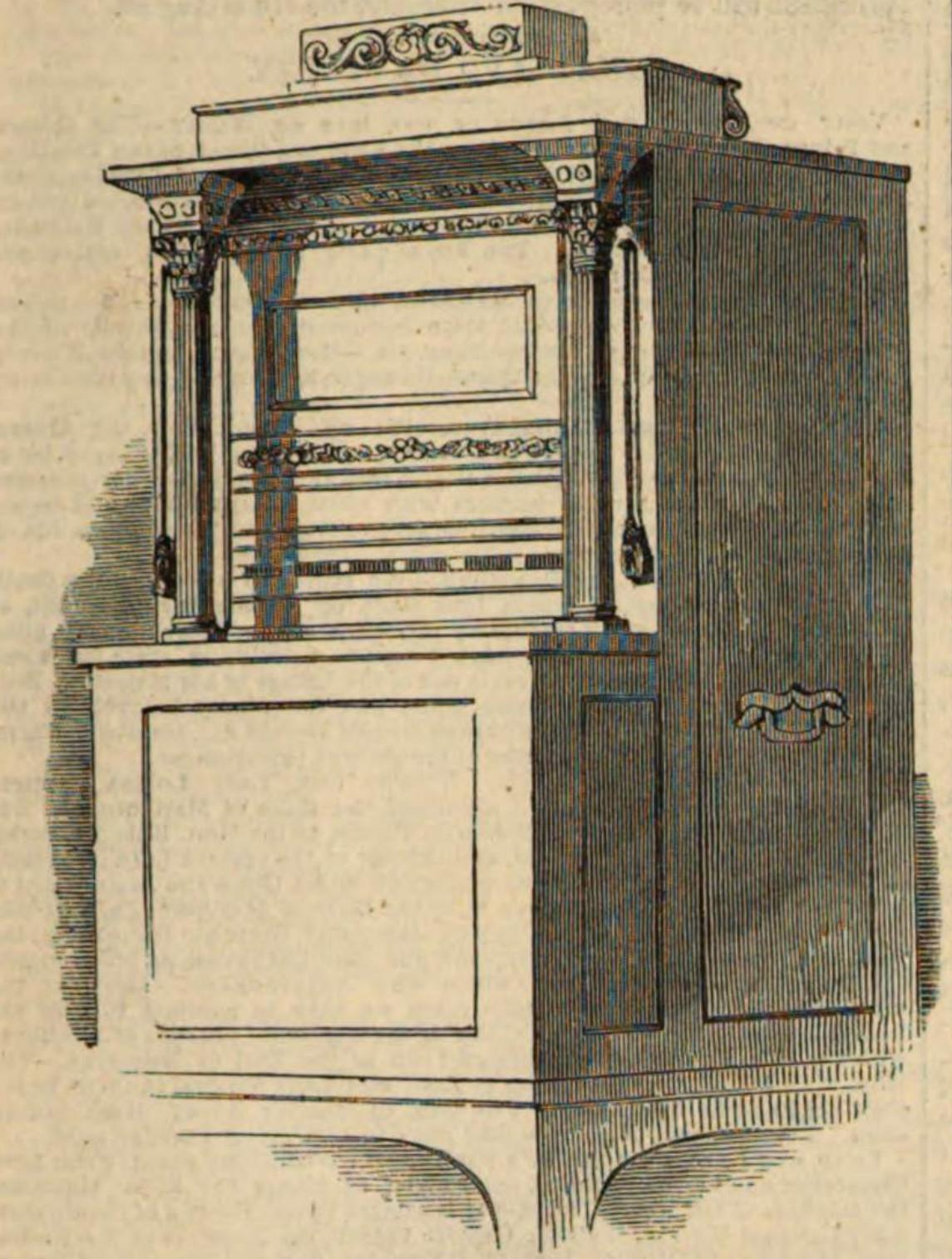
尤里卡（Eureka）

1843年，诗人拜伦之女、英国数学家艾达·洛夫勒斯（Ada Lovelace）写下了计算机科学史上的第一条编程算法。1830-1840年间，约翰·克拉克（John Cark）制造了一台会写拉丁文诗歌的写作机器，它被称为“拉丁六步格诗机器人（Latin Hexameter Automaton）”或“尤里卡（Eureka）”。尤里卡是一种简单机械自动机，只要机械运动力保持在活动状态，它就能借助它执行某些动作。当启动时，尤里卡便会一个接一个地生成拉丁六音步，直到一个为齿轮、滑轮和飞轮提供动力的下降的铅锤落下来。

图灵机模型

1936年，英国计算机科学家阿兰·图灵（Alan Turing）描述了一种自动机器，它分为三个部分：一条无限长的纸带，一个可以在纸带上左右移动的读写头，一套控制规则的表。[1]图灵机可以被看作写作自动化的肇始，彼时写作被递减为一种数据写入行为；也正因为此，写作开始与阅读更紧密地结合在语言行动当中。

1960年代，对话式机器人ELIZA问世。它是一个早期处理自然语言的计算程序，由MIT人工智能实验室的约瑟夫·维泽鲍姆（Joseph Weizenbaum）制造。ELIZA所用的是“模式匹配（pattern matching）”方法。当你对着ELIZA说话时，它会像理疗学家一样基于你自己的话进行反应。例如如下对话：

——“你好，我是ELIZA。”

——“你是第一个自动化作者吗？”

——“你为什么感兴趣于我是不是第一个自动化作者？”

——“我正在做一些研究。”

——“你做研究多久了？”[2]

德国媒介学者基特勒（Friedrich Kittler）将计算机作为信息世界的普遍符号机器，它将此前媒介的激增转化为一种内爆，计算机器集成着具有操作性的数学媒介（存储，传输，计算）。[3]作为一种数据写入行为的写作，以计算机器为基础设施，构建着机器丛中庞大的语义网络。当斯蒂格勒（Bernard Stiegler）在论述“自动化社会”时，写作俨然成为了信息与工业外显化的记忆科技（mnemotechnology）。[4]人工智能技术的发展，加速着算法治理，将写作这一古老的文化技艺愈发外显化为记忆科技。

空格与象形

1948-1950年间，数学家、电子工程师和密码学家克劳德·香农（Claude E. Shannon）采用统计学方法对英文进行了一系列实验，它们被称作“印刷英文”（Printed English）。二战期间，香农加入了贝尔实验室（Nokia Bell Labs）。他于1948年发表的论文《通信的数学原理》（A Mathematical Theory of Communication）奠定了现代信息论的基础。在随后与数学家沃伦·韦弗（Warren Weaver）合著的同名专著中，香农将他的信息理论延伸到了对英语文字的实验。

香农和韦弗二人通过对字母顺序进行数学的近似值计算，描述了一种英语文字的冗余。在对英文的零级近似值计算中，独立且具有同等可能性的字母以一种随机连接出现：“XFOML RXKHRJFFJUJZLPWCFWKCYJ FFJEYVKCQSGHYD QPAAMKBZAACIBZ HJQD”。通过第二级近似值计算，出现了一些可以识别的词组，并可以读出语义：“THE HEAD AND IN FRONTAL ATTACK ON AN ENGLISH WRITER THAT THE CHARACTER OF THIS POINT IS THEREFORE ANOTHER METHOD FOR THE LETTERS THAT THE TIME OF WHO EVER TOLD THE PROBLEM FOR AN UNEXPECTED”。[5]

如何读懂语义？香农与韦弗的初衷是以统计学结构来描绘和定义字母及其音素/音位单元，这意味着，并非词组在制造意义，而是字母间的空格区隔着、支撑着统计学结构，以此制造着语义；它将字母赋予为印刷符号，区别于书写符号。香农的这一论断来自于他对图灵机的解读，他将图灵机纸带上的方框称为“一个特别的空符号”，并将其称之为第二十七个字母。[6]进一步而言，这一非字母的离散空格为字母文字在数字与计算技术条件下赋予了新的科技特性与功能。

学者刘禾（Lydia H. Liu）追溯了另一条有关香农的思想实验的重要线索，即文学理论与实践中关于象形（ideograph）的探讨。延续乔伊斯、马拉美、庞德甚至维特根斯坦对象形的研究传统，象形系统，或图像写作，指的是一种对字母和词汇的视觉认识方式，即在阅读过程中如何挑拣字母或词汇从而生成语义（不）确定性。香农与韦弗的“印刷英文”则将这种视觉化与拼音化带进了以空格为基础的统计学结构中。刘禾指出，以0/1为表示的象形系统使得印刷英文成为了一种普世语言，它将世界上的其他语言都变为了它的翻译版本。[7]这一对印刷英文的论述也暗示着韦弗在冷战和控制论思维中对计算机的算法诉求，即追求一种完满计算和透明翻译，假设一种普世性语言的逻辑结构能够应对任何的翻译问题，并对通信的普遍问题进行回应。

回到操作型媒介与语言之中，德国媒介哲学家西贝尔·克莱默（Sybille Krämer）介绍了另一种象形与空格在计算机的操作型写作中的表征方式。她强调，诸如文字与图像等各种象形系统可以表征算法中的数学公式与计算，这种指涉性（referential）的计算生成机制塑造着人的感知。象形系统在此塑造着从数字算法到符号层面的连续性感知。虽然克莱默的这一操作型写作仍然强调象形系统的模拟能力，但相较于印刷英语而言，操作型写作暗示了标记符号物质性（notational materiality）的多样化，为我们思考人机关系中的媒介语言提供了基础。

媒介语言

早在计算机中的印刷英语及其位值出现前，图像诗歌就有着对于空格的应用传统。1897年，法国象征主义诗人马拉美（Stéphane Mallarmé）出版了他的著名诗歌“Un Coup de dés jamais n'abolira le hasard”（A Throw of the Dice will Never Abolish Chance，《骰子一掷，不会改变偶然》）。这首诗采用了不同寻常的印刷排版方式，并紧密结合自由韵律。它促使了20世纪平面设计与具象诗歌（concrete poetry）的交汇与兴起。

马拉美手稿

这首诗首先发表在Cosmopolis期刊，它有20页长，空白页上布满了各种字体字型。每翻开的两页作为诗的一组；文本沿着不规则的线条分布。马拉美的这一设计意在引导读者注意页面空白以及词语之间的空白。它颠覆了背景与前景的关系，并且使得页面这一文本的物质载体得以问题化：空间位值成为了诗歌自身意义生成的力量。[8]这意味着，字词的排版位值和它们彼此之间的距离成为了塑造意义的媒介。进一步而言，马拉美还赋予了词语多样的视觉特点，比如不同的字型和字体。这些视觉因素成为了阅读和阐释诗歌意义的一部分。

美国哲学家纳尔逊·古德曼（Nelson Goodman）描述过一种意义生产的地带，即符号的空间位值通过将图像介绍进入文本领域，从而扩展了诗歌的表意范畴。图像诗歌融合了两种审美特质：一是古德曼所称的“浓厚而连续的”图像符号系统，二是依赖空格来操作的文字系统。古德曼区分道，图像符号以语境而连接，它们的意义依赖于它们与其它记号符的关系，因而它是模拟的；而书写符号是可转印的，它们是数字的、分离的、由空格符组成的。

回到操作型写作中，克莱默援引了古德曼关于图像与文字符号的论点，来支持她的操作型写作中记号符的图像性（notational iconicity）特征，即计算性文本可以使得其空间中的认知秩序可见。对于操作型写作而言，这一图像性指的不仅仅是计算的数字矩阵与文本中字母的运用，还有空间中的其他使得秩序可见的因素，例如标题、小结、斜体字等。它们使得概念的差异化变得可能。

虽然克莱默所主张的操作型写作仍局限于记号符的图像性，但其中的位值至少说明了记号符的物质性。本文对于记号符及其位值所组成的媒介语言的主张，不同于克莱默基于图像性的认知连续性的认识，也试图逾越刘禾所宣称的计算机器中印刷英语的象形统治地位。记号符及其位值强调媒介语言的物质特殊性，而它能够引发的认知是连续的抑或离散的，则存在于机器如何调动媒介语言的操作过程之中。这一操作型写作所触发的认知体验往往交杂着连续和离散的多样态。这即是说，自动写作的美学体验，存在于写作机器的媒介语言所塑造的多样态之中。

自动写作的史前史和早期历史，与印刷术在文学中的开拓性运用和在计算机器中的自然语言处理彼此交织。记号符及其位值为我们提供了一种理解自动写作中的媒介语言的基本要素。记号符、位值和操作型写作，共同构成着自动写作的媒介语言。反之，媒介语言也成为了认知与体验自动写作的关键概念。进一步而言，这一媒介语言也开启了对自动写作中的文字（或图像）的生成机制的继续探究。

参考文献

[1]. Turing, Alan. “On Computable Numbers, with an Application to the Entscheidungs Problem.” In The Essential Turing, edited by B. Jack Copeland, 58–90. Oxford: Clarendon Press, 2004.

[2]. Alexander, Anne, Caroline Bassett, Alan Blackwell, and Jo Lindsay Walton. Ghosts, Robots, Automatic Writing: An AI Level Study Guide. Cambridge: Cambridge Digital Humanities, 2021. www.cdh.cam.ac.uk.

[3]. Kittler, Friedrich. “The World of the Symbolic: A World of the Machine.” In Literature, Media, Information Systems: Essays, edited by John Johnston, 130–46. Oxon & New York: Routledge, 1997.

[4]. Stiegler, Bernard. “Memory.” In Critical Terms for Media Studies, edited by W. J. T. Mitchell and Mark B. N. Hansen, 66–87. Chicago & London: University of Chicago Press, 2010.

[5]. Shannon, Claude, E., and Warren Weaver. The Mathematical Theory of Communication. The University of Illinois. USA: The University of Illinois, 1964, pp. 43–44.

[6]. Shannon, Claude, E. “A Universal Turing Machine with Two Internal States,” Claude E. Shannon: Collected Papers, edited by N. J. A. Sloane and Aaron D. Wyner, 733. <https://ieeexplore.ieee.org/document/5311596>.

[7]. Liu, Lydia H. “ISpace: Printed English after Joyce, Shannon, and Derrida.” Critical Inquiry 32, no. 3 (2006): 516–50.

[8]. Knowles, Kim, Anna Katharina Schaffner, Ulrich Weger, and Andrew Michael Roberts. “Reading Space in Visual Poetry: New Cognitive Perspectives.” Writing Technologies 4 (2012): 75–106.