数学家发现了爱因斯坦瓦片，它可以无限铺满一个平面而不会重复

数学家们发明了一种新的13边形，可以无限地铺满一个平面，而不会出现重复的图案。他们称之为“爱因斯坦瓦片”。这个词并不是来自著名的物理学家阿尔伯特·爱因斯坦，而是来自他姓氏的德语翻译：一块石头。

数学家们对这个问题感兴趣已经有几十年了。早在1961年，数学家王浩就提出了一个猜想，认为无周期平铺，即永远不会成为重复图案的平铺，是不可能的。但他自己的学生罗伯特·伯格尔却证明了他错了，他找到了一组20,426个形状，当仔细排列时，永远不会重复。

他后来将这个集合缩减到了104个瓦片。这意味着如果你买了一套这样的瓦片，你可以把它们排列在你的厨房地板上，永远不会找到一个重复的图案。

彭罗斯平铺包含多种对称性，但它永远无法周期性重复。

在20世纪70年代，诺贝尔奖获得者、物理学家罗杰·彭罗斯发现了一组只有两个瓦片的集合，它们可以以非重复的方式排列在一起，现在被称为彭罗斯平铺。

从那时起，世界各地的数学家们都在寻找无周期平铺的圣杯，“爱因斯坦瓦片”。他们是否能找到一种单一的形状能够填充一个二维空间，而不会重复它所创造的图案呢？

答案刚刚被英国东约克郡一位退休印刷技术员大卫·史密斯发现了。他是如何发现这个惊人的解决方案的呢？“我总是在摆弄和实验各种形状，”史密斯告诉《纽约时报》。

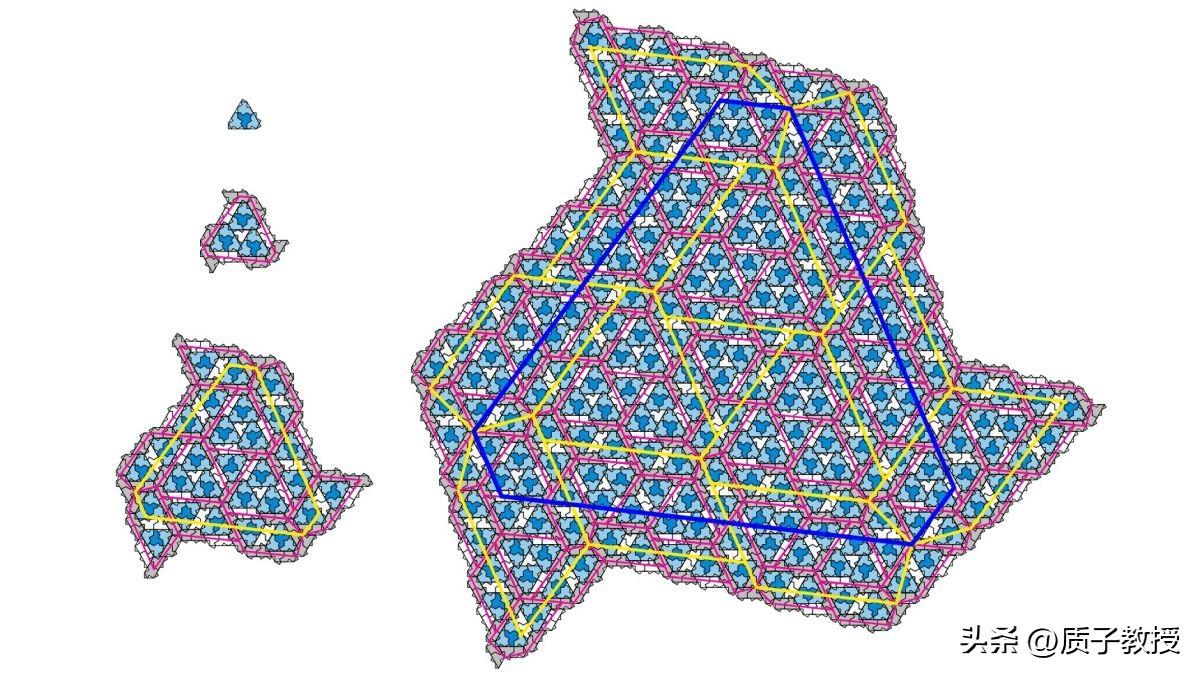
史密斯发现了一个13边形（也称为十三角形），它有一个特殊的性质：它可以被分成四个更小的相同形状（称为子瓦片），或者可以被组合成四个更大的相同形状（称为超级瓦片）。这意味着这个13边形可以无限地缩小或放大，并且可以用来铺满一个平面，而不会出现重复的图案。这就是“爱因斯坦瓦片”的定义。

史密斯的发现是数学界的一个重大突破，也是一个美丽的艺术作品。他的13边形有着复杂而优雅的对称性，可以创造出令人惊叹的图形。他还给他的形状起了一个有趣的名字：帽子（hat），因为它看起来像一个戴着帽子的人的轮廓。

史密斯并不是一个专业的数学家，但他对形状和图案有着浓厚的兴趣。他曾经设计过一种新型的拼图，叫做“史密斯拼图”，它由一些不规则的形状组成，可以拼成任何你想要的图案。他还曾经发明过一种新型的骰子，叫做“史密斯骰子”，它由一些不同形状的多面体组成，可以用来玩各种游戏。

史密斯说，他对“爱因斯坦瓦片”的灵感来自于一本关于无周期平铺的书籍，以及一些网上的资源。他用电脑软件来设计和测试他的形状，并与一些数学家和艺术家交流他的想法。他说，他花了大约两年的时间才找到了这个13边形，并证明了它是一个“爱因斯坦瓦片”。

史密斯说，他对自己的发现感到非常兴奋和自豪。“我觉得我做了一件很特别的事情，”他说，“我觉得我创造了一种新的美。”

史密斯和他的合作者们已经将他们的发现发表在了数学杂志《几何与拓扑》上，并得到了其他数学家们的认可和赞扬。他们还计划制作一些实体模型，以展示他们的形状在三维空间中是如何排列和变化的。

史密斯说，他希望他的发现能够激发更多人对数学和艺术之间的联系感兴趣，并且能够为未来可能有用的应用打开新的可能性。“我认为这是一个很有价值和有趣的领域，”他说，“我希望能够继续探索和创造更多。”

Sutter, P. (2023). Newly discovered ‘einstein’ tile is a 13-sided shape that solves a decades-old math problem. Live Science. Retrieved from https://www.livescience.com/newly-discovered-einstein-tile-is-a-13-sided-shape-that-solves-a-decades-old-math-problemSmith, D., Mannan, M., & Sadun, L. (2023). The first known example of an einstein. Geometry & Topology, 27(1), 1-25. doi:10.2140/gt.2023.27.1Penrose, R. (1974). The role of aesthetics in pure and applied mathematical research. Bulletin of the Institute of Mathematics and its Applications, 10(7/8), 266-271.Berger, R. (1966). The undecidability of the domino problem. Memoirs of the American Mathematical Society, 66, 1-72.Wang, H. (1961). Proving theorems by pattern recognition II. Bell System Technical Journal, 40(1), 1-42.