数学里的自然常数e，被大神欧拉完美解决（欧拉数）

在数学领域，有许多有趣的常数，这些常数的起源一般都经历了波澜壮阔的数学进化史。比如我们之前提到的圆周率，这是比较常见的，小学阶段也能遇到。

今天我们要学的是自然常数e，这很重要。和π一样，它是一个无限的、非循环的小数。我们至少要在高中接触对数函数后才会接触到这个数，而要想完全了解这个数，至少要在大学学习高等数学。自然常数E经常出现在数学物理计算中，那么这样一个重要而特殊的数是怎么来的，又有哪些具体的实际意义呢？

在十八世纪初，有一位伟大的数学神，名叫欧拉。这个大家应该都很熟悉。他绝对是人类历史上最强大的五位数学家之一。自然常数E是这位数学家在求解复利问题时提出来的，因此E也被称为欧拉数。当n接近无穷大时，(1 1/n)n不是接近无穷大，而是等于2.71828这样的常数，这是一个无限的、非循环的小数，它像圆周率一样是无理的。后来为了便于记录，用字母E表示。

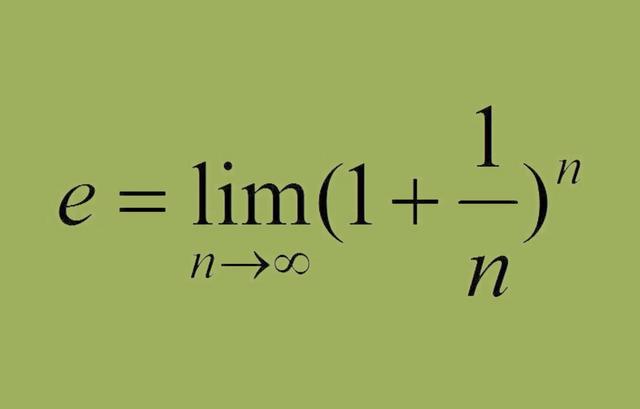
这个E是现在大家都习惯和常用的自然常量。E不是随机数。随着你对数学的学习越来越深入，你会逐渐发现它是数学中最有用的数字之一。当我们用镜像法画出y=ex的函数时，会发现对于这个函数曲线上的任意一点，它的斜率也是ex，也就是说y=ex的导数就是它自己。

不仅如此，这个函数的图围绕X轴的面积也是E X,而在函数y=n X中，只有当n=E时，这个方程才有这样神奇的性质。从这些例子中我们不难看出，自然常数e无疑是微积分领域中一个重要而特殊的数。

不仅如此，在物理学领域，自然常数E的应用也很广泛，通常以正态分布或与波有关的公式出现，如电磁波、声波、量子波等。除了上面的例子外，关于自然常数e还有一个非常著名的方程，即欧拉方程，也叫欧拉恒等式:e(iπ) 1=0。这个公式可以说是数学发展至今出现的最漂亮的公式。这个公式同时完美地连接了数学中最重要的数。