数学中最大的陷阱,毁掉无数数学天才,却有着不可抗拒的魔力
这是数学界一个充满神秘的难题。这个看似简单的问题,却一直困扰着数学家们,至今尚无法找到一个满意的解答。
这个问题的核心内容是这样的:从任意一个正整数开始,如果这个数是偶数,就将其除以2;如果是奇数,则乘以3再加1。然后对所得的结果重复以上步骤。关于这个问题的猜想认为,无论我们从哪个正整数出发,最终都会达到数字1(进入一个4,2,1的循环)。举个例子,任意选一个数字,比如7。应用这两个规则:
如果数字是奇数,我们乘以3再加1,所以3乘以7是21,加1是22。
如果数字是偶数,我们除以2,所以22除以2是11。
继续应用这两个规则。11是奇数,所以乘以3得到33,再加1得到34。偶数除以2得到17。奇数乘以3得到51,加1得到52。偶数除以2得到26,还是偶数除以2得到13。奇数乘以3得到39,加1得到40,偶数除以2得到20,除以2得到10,除以2得到5。奇数乘以3得到15,加1得到16,除以2得到8,然后是4、2和1。
7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
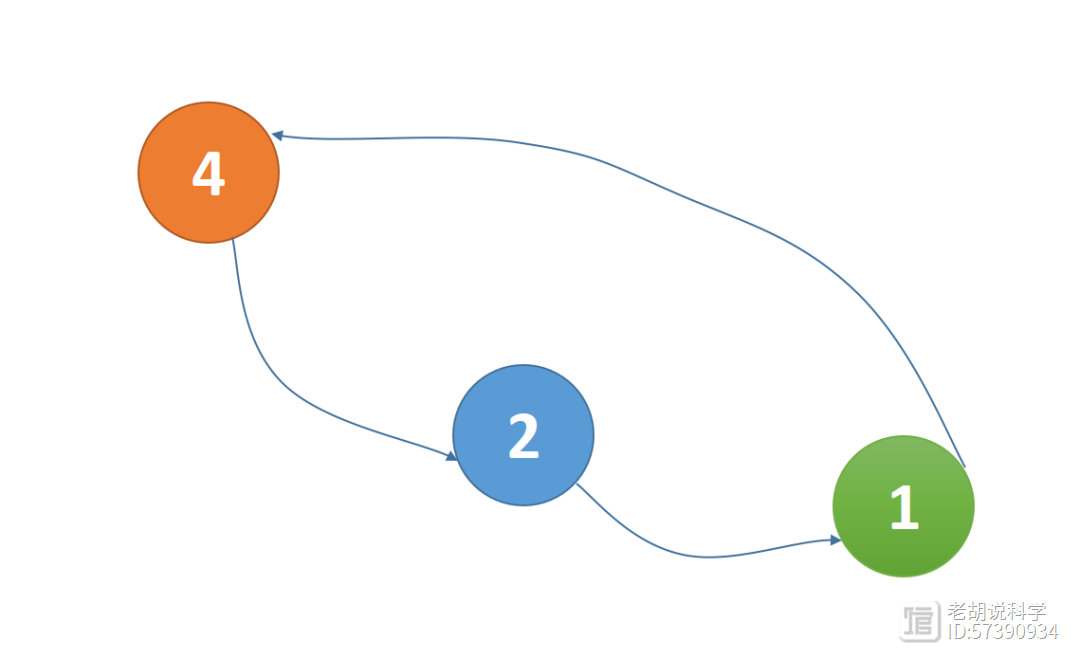
1是奇数,所乘以3再加1,结果等于4。然后4可以变成2,2可以变成1,从而进入了一个4,2,1的循环。
这个猜想被称为科拉茨猜想(Collatz conjecture),也被称为3X 1猜想。通过应用3x 1得到的数字被称为冰雹数(hailstone numbers),因为它们像雷暴云中的冰雹一样上下起伏,但最终都会降到1。

你可以把这些数字想象成高度(以米为单位),表示在地面以上的高度。所以像26这样的数字开始时离地面26米高,如果应用3x 1,它会升到40米的高度,在总共在10步内降到1。
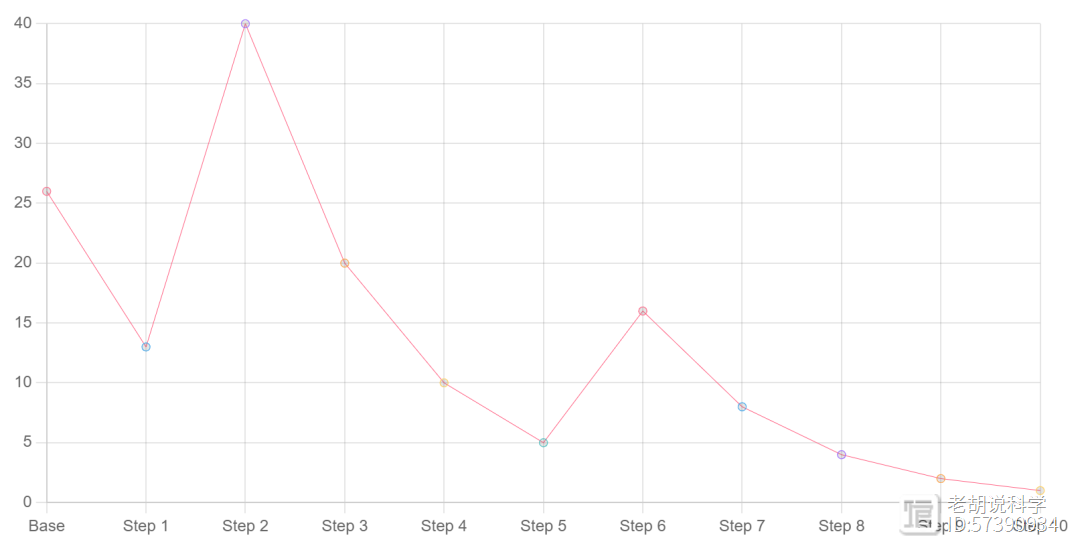
所以10被称为它的总停止时间。但是,如果选择数字27,它就会跳来跳去,一直上升到9232,比珠穆朗玛峰还要高,然后它也会降回地面1。总共需要111步才能让27降到1,最终陷入4-2-1循环。不同数字的路径变化非常大,即使是紧挨着的数字如26和27。
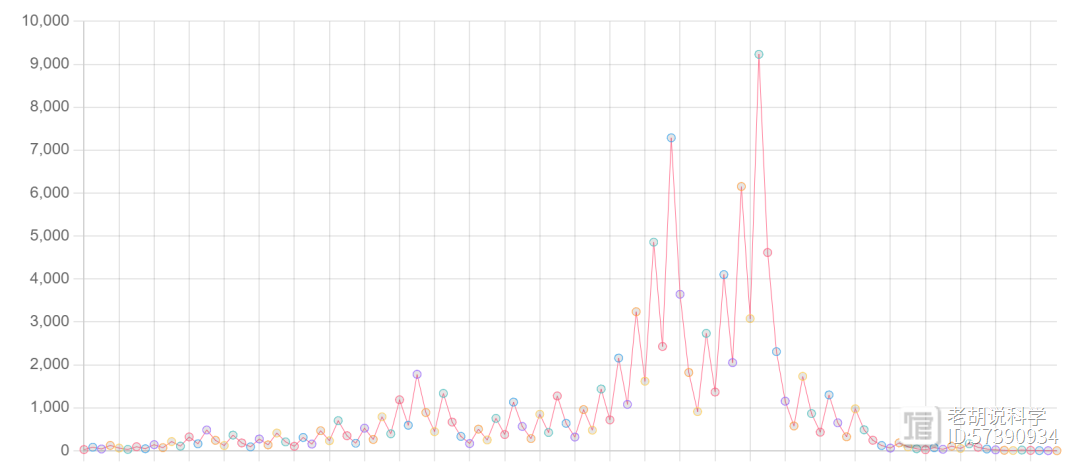
那么,如何解决这个问题呢?

jeffrey legarius是3x 1问题的世界权威。他告诫他的学生
如果你想要事业,那就不要研究这个问题。不要花时间写关于这个问题的文章或发表关于这个问题的论文。先做一些实际的数学工作。
他的一个学生alex conterovich没有听从他的建议,研究了冰雹数的路径,看是否有规律。显然,所有数最终都会回到1,但是它们回到1的过程如何呢?模式是随机的。
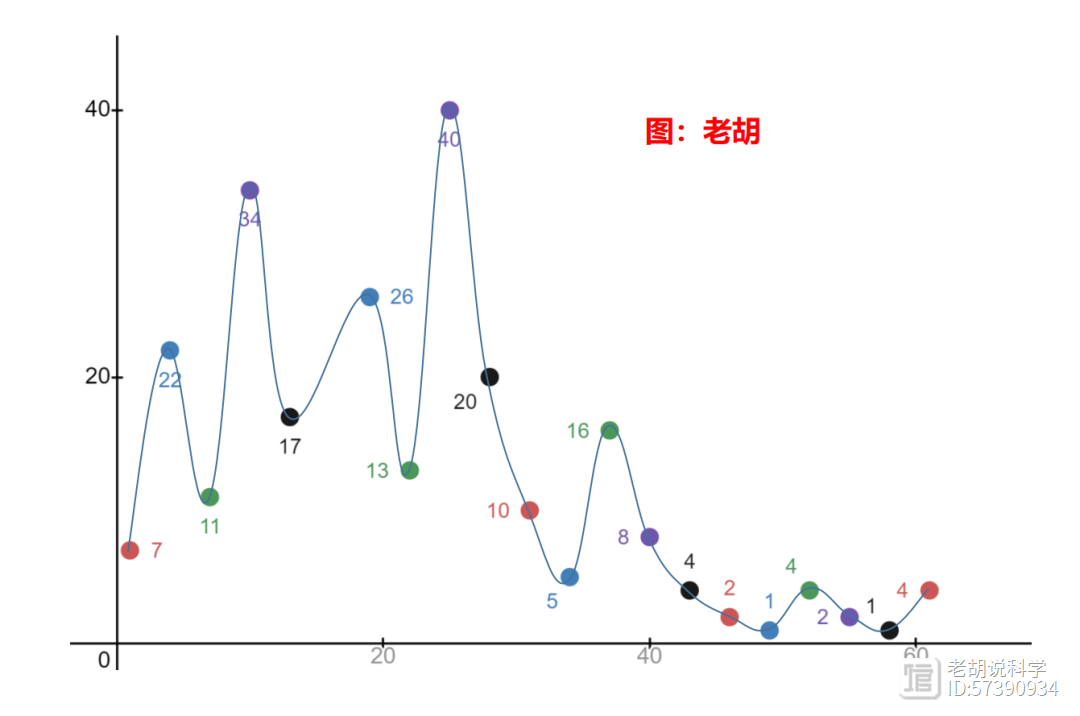
下面是一个随机选择的大数字的回到1的路径。
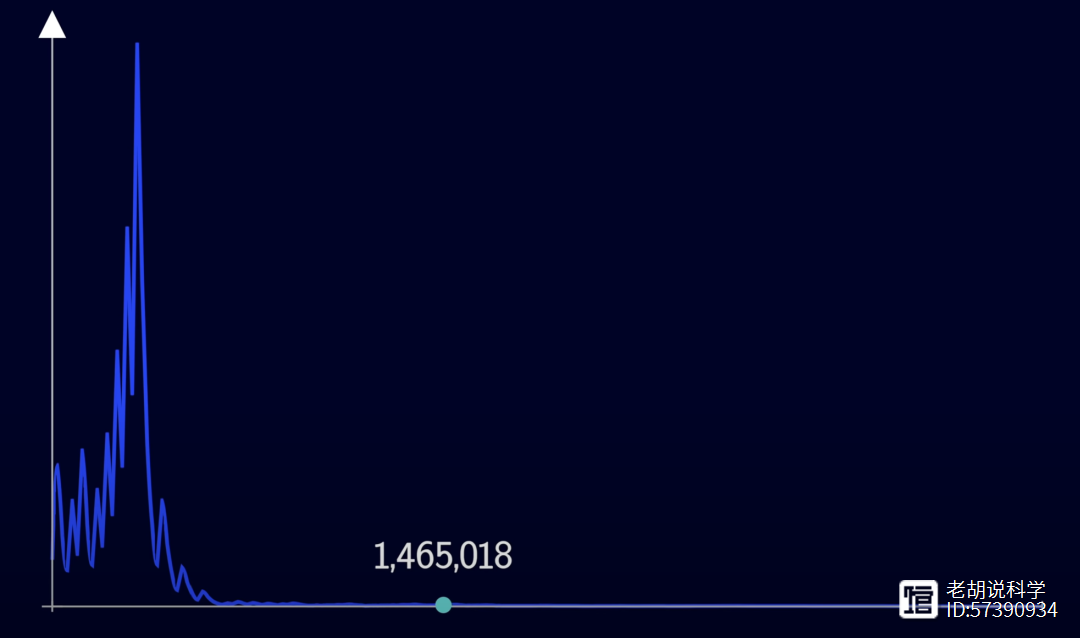
图形先是达到峰值,然后很快下降,后面的数字在这个尺度上几乎无法看清楚。但是,如果取对数,你会发现这个曲线图有一个向下的趋势。

这并非巧合,它是几何布朗运动的例子。这意味着,如果取对数并消除线性趋势,波动是随机的。
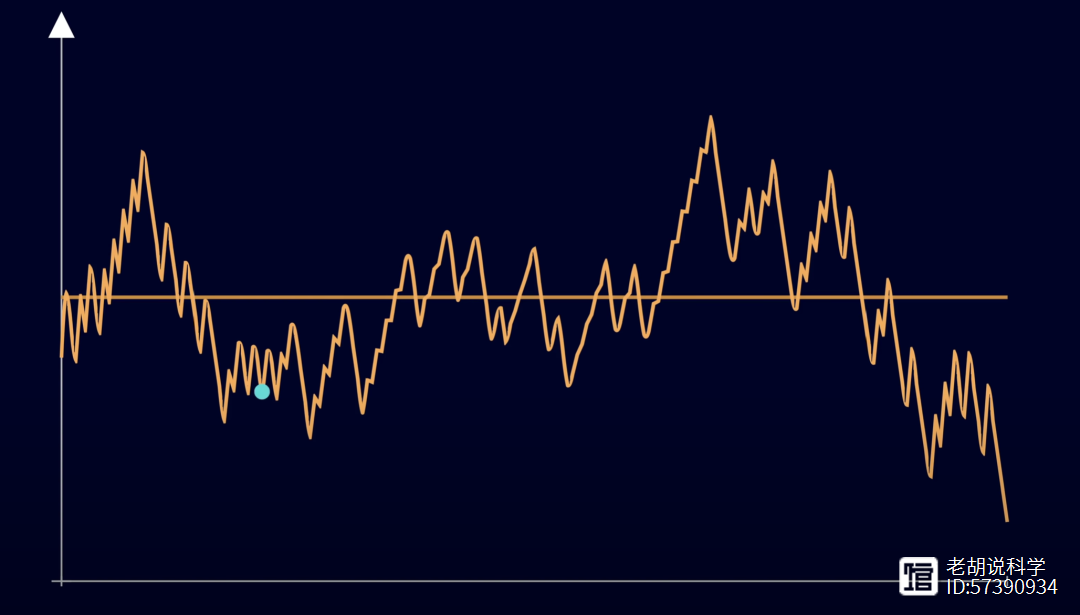
这就像在抛掷硬币。如果硬币是正面,线条上升;如果是反面,线条下降。3x 1就像股市的随机波动,只不过长时间内股市趋势是上升的,而3x 1趋势是下降的。
分析3x 1的另一种方法是观察序列中每个数字的最高位数。比如120最高位数字是1,934最高位数字是9。下面是以3为起始的冰雹数,
10→5→16→8→4→ 2→ 1
我们可以数出有多少数字以1开头,有多少数字以2开头,有多少数字以3开头等等,做一个直方图。
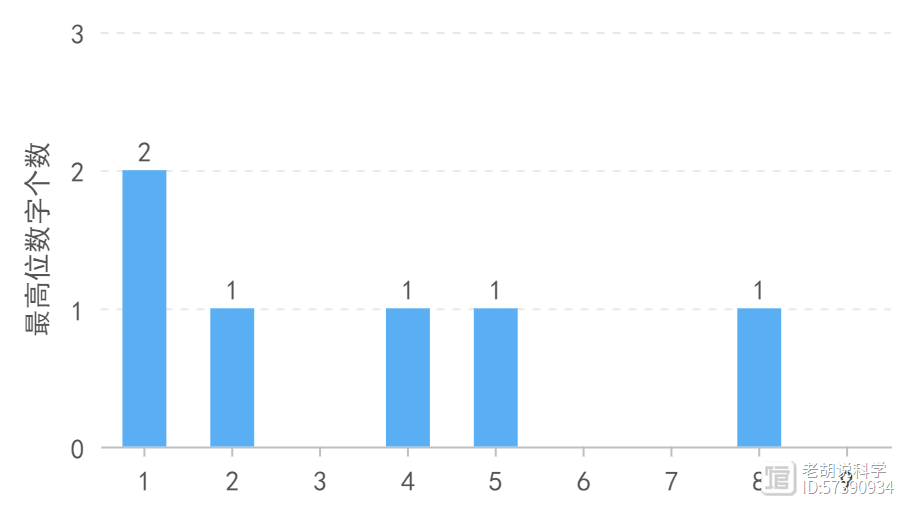
我们可以对以4为起始的序列做同样的事情,对于以5、6和7为起始的序列,我们同样可以统计以每个数字1到9为开头的数字数量,并画出直方图。如果继续为越来越大的数字做这个操作,最终直方图会稳定下来。
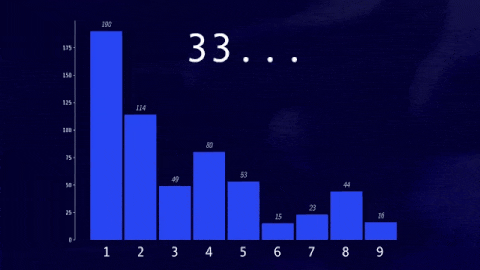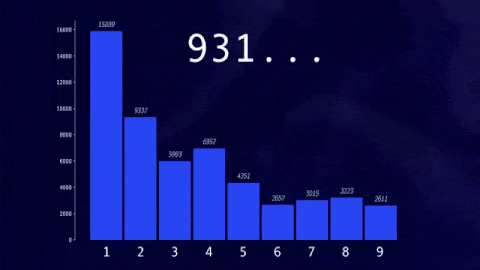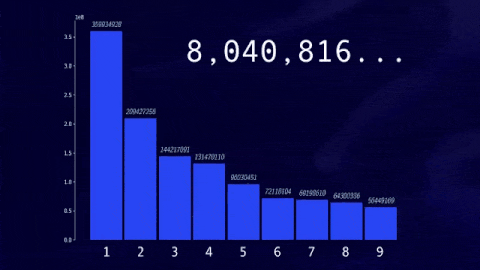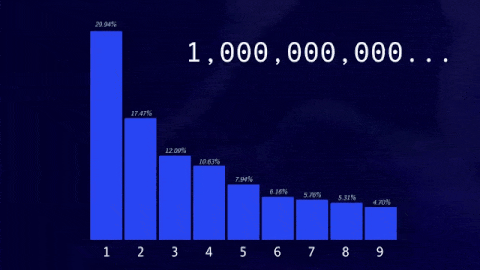
对于前十亿个序列,你会发现1是最常见的最高位数字,30%的数字以1开头,约17.5%的数字以2开头,12%的数字以3开头,更高位数字的频率逐渐降低,不到5%的数字以9开头。
这种模式不是3x 1独有的,实际上它在各个领域都有出现,从国家人口到公司价值,以及物理常数和斐波那契数列等等。
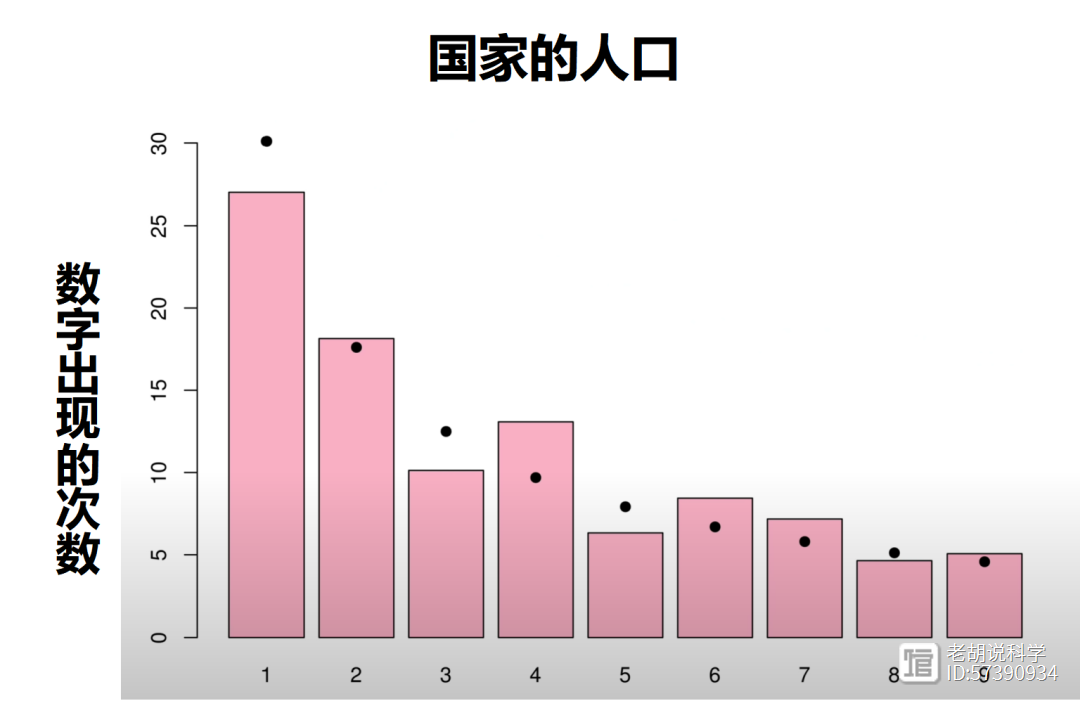
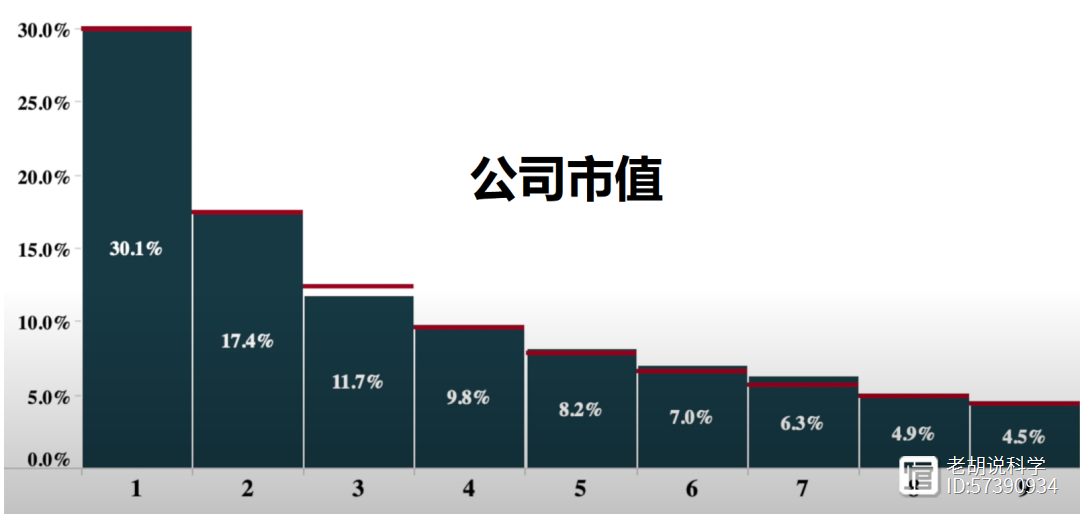
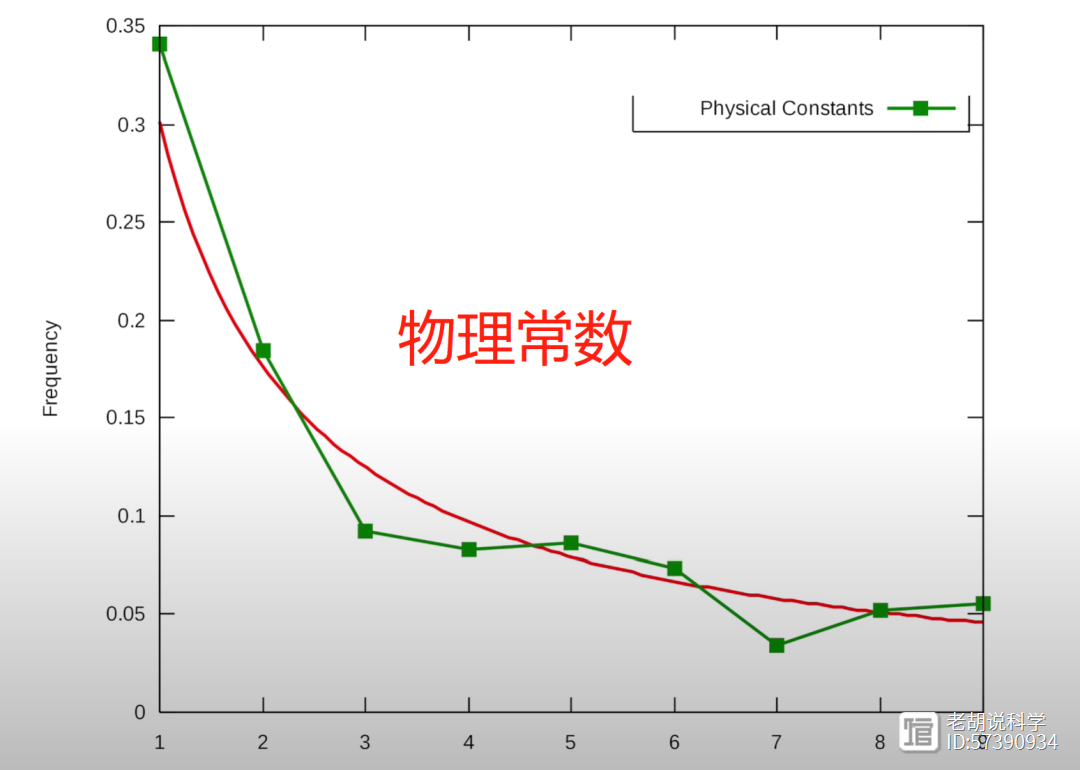
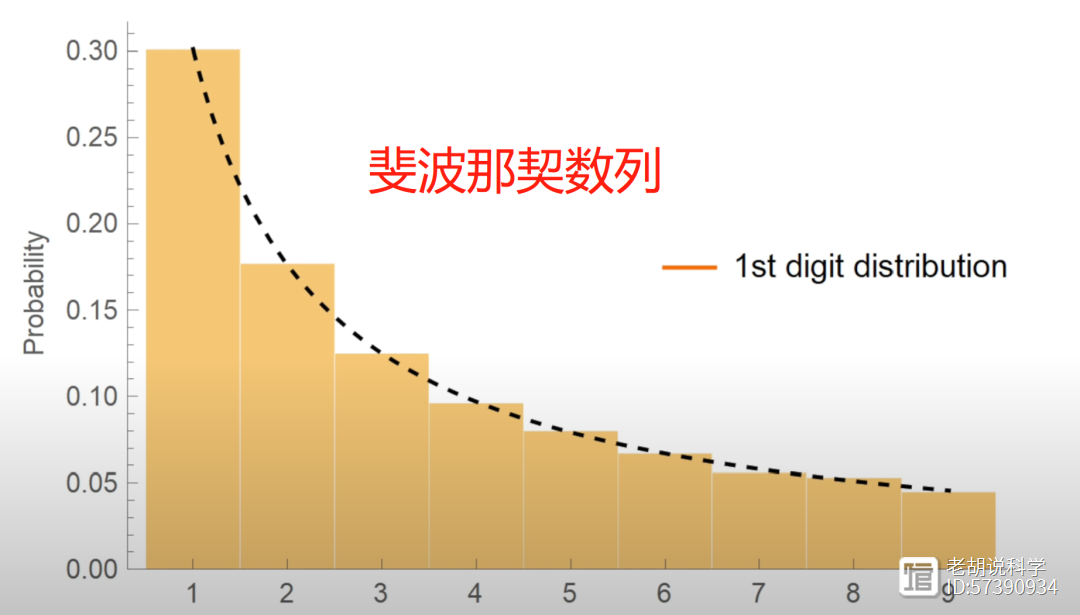
这种分布被称为本福特定律(benford'slaw),它甚至可以用于检测欺诈。如果你的所得税表格上的所有数字都符合本福特定律,那么你可能是诚实的;如果不符合,你可能在隐藏一些事情。在选举中,本福特定律可用于发现违规行为。当涉及的数字跨越几个数量级时,本福特定律效果最佳,正如3x 1所涉及的数字。
但是本福特定律无法告诉我们所有的数字是否都会陷入4-2-1循环。为此,我们需要另一种分析方法。乍一看,当应用3x 1时,所有数字都应该以1为终点,这似乎很奇怪。因为,奇数和偶数的数量是相同的,但奇数增加了三倍加1,而偶数只是减半。
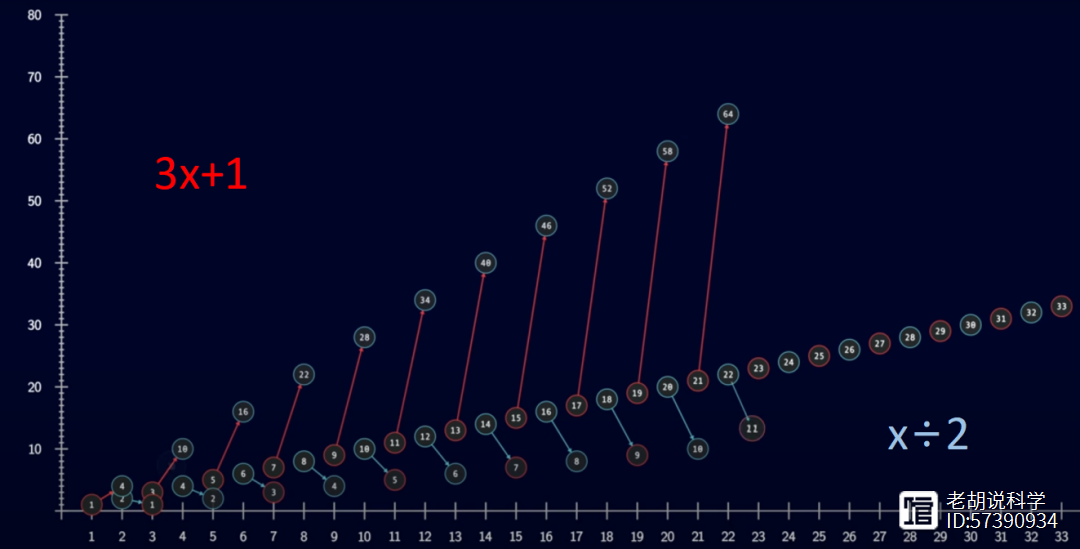
因此,平均来说,每个序列似乎应该增长而不是缩小。但是问题在于,每次将奇数乘以3然后加1,它总是变成偶数,这意味着下一步是除以2。所以奇数实际上并没有通过3x 1增加三倍,它们增加了约3/2的因子(忽略了加1,因为对于大数来说它无关紧要)。
实际上,3/2是奇数在一步内增长的最大程度。想一想从序列中的一个奇数到下一个奇数的路径,在乘以3并加1之后,得到一个偶数,50%的情况除以2会得到一个奇数。但是有四分之一的情况,可以在得到下一个奇数之前除以4,所以有四分之一的数字,序列中的下一个数字将是其初始值的四分之三。有八分之一的情况,可以在得到下一个奇数之前除以8,有十六分之一的情况,可以在得到下一个奇数之前除以16等等。

如果取几何平均数,你会发现平均来说,要从一个奇数到下一个奇数,需要乘以3/4,这个值小于1,
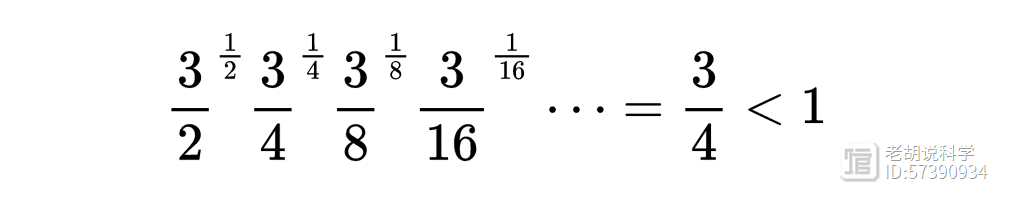
所以从统计上讲,3x 1序列更可能缩小而不是增长。
以341为例,乘以3再加1,得到1024,除以2,然后再除以2,再除以2,再除以2,一共十次,直到减少到1。
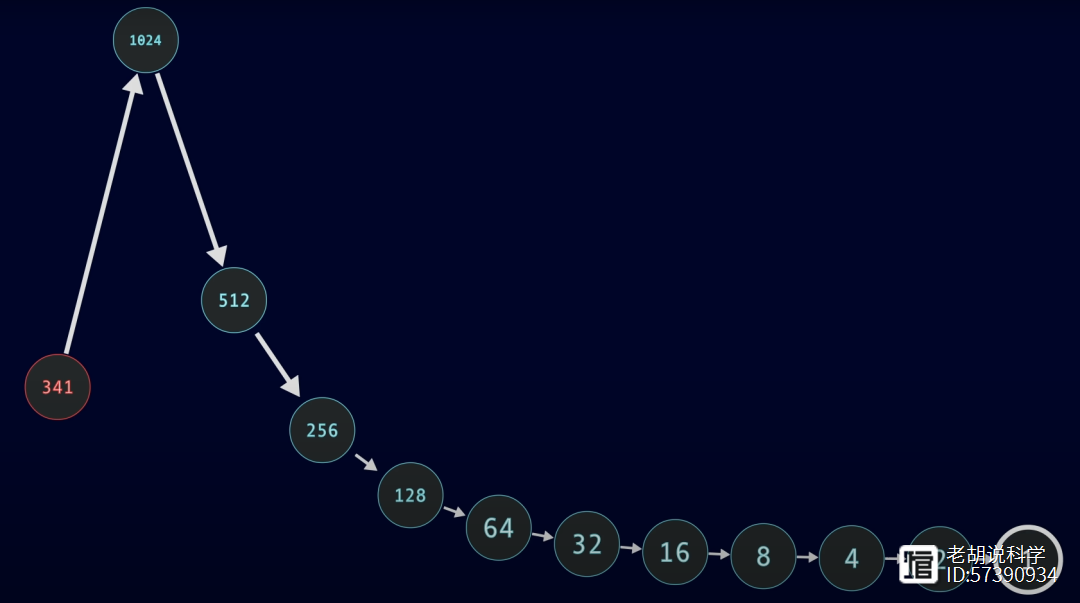
可视化3x 1中数字路径的一种方法就是简单地展示每个数字如何连接到序列中的下一个数字,这被称为有向图(directed graph)

它看起来像一棵树。如果猜想成立,这意味着每个数字都会连接到这个图,一直到无穷大,最终都汇入到4-2-1的巨大河流中。
一些数学家通过将每个数字逆时针旋转(如果是奇数)和顺时针旋转(如果是偶数)来修改这种可视化。然后你得到一个看起来像珊瑚或海藻的结构。通过调整奇数和偶数的旋转角度,你可以创建出这些美丽的有机形状。

现在,猜想可能有两种错误的方式:可能存在以某个数字开始的数字序列,它们会无限增长。出于某种原因,它不遵循所有其他数字所遵循的数值规律。另一种可能性是存在一个数字序列,形成一个封闭的循环。这个循环中的所有数字都与主图无关。
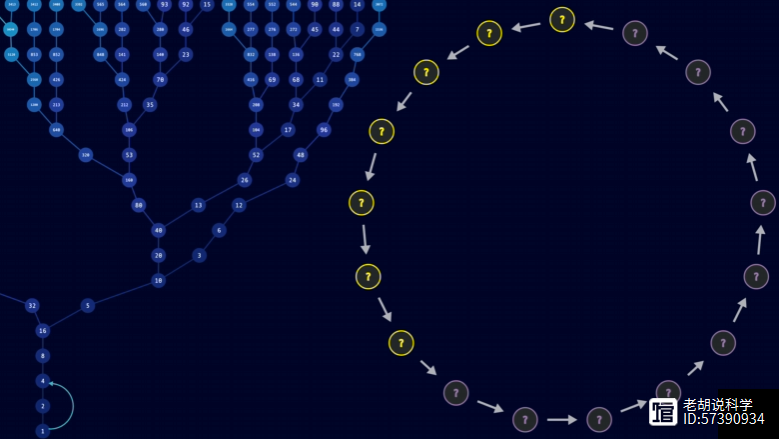
然而,到目前为止,尽管已经进行了大量尝试,但仍未发现任何通往无穷大的序列或循环。数学家们已经暴力测试了所有小于2的68次方的数字,没有一个能推翻这个猜想。
因此,猜想很可能是正确的,但还没有被证明。数学家尝试证明这一猜想的一种方法是制作散点图,x轴表示所有的初始数字(种子数字),y轴表示每个序列中的一个数字。现在,如果你可以证明在每个3x 1序列中都有一个比原始种子数字小的数字,那么你就证明了Collatz猜想,因为无论你选择哪个数字,你都知道它在某个时候会变得更小,而这个更小的数字作为种子也会变得更小,如此重复直到1,这意味着任何序列的唯一结束方式都是4-2-1循环。

虽然尚未证明这一点,但在1976年,Rijoteras证明了几乎所有的Collatz序列都能达到低于初始值的点。1979年,这个极限被降低,几乎所有序列都能达到低于x的0.869次方的点。
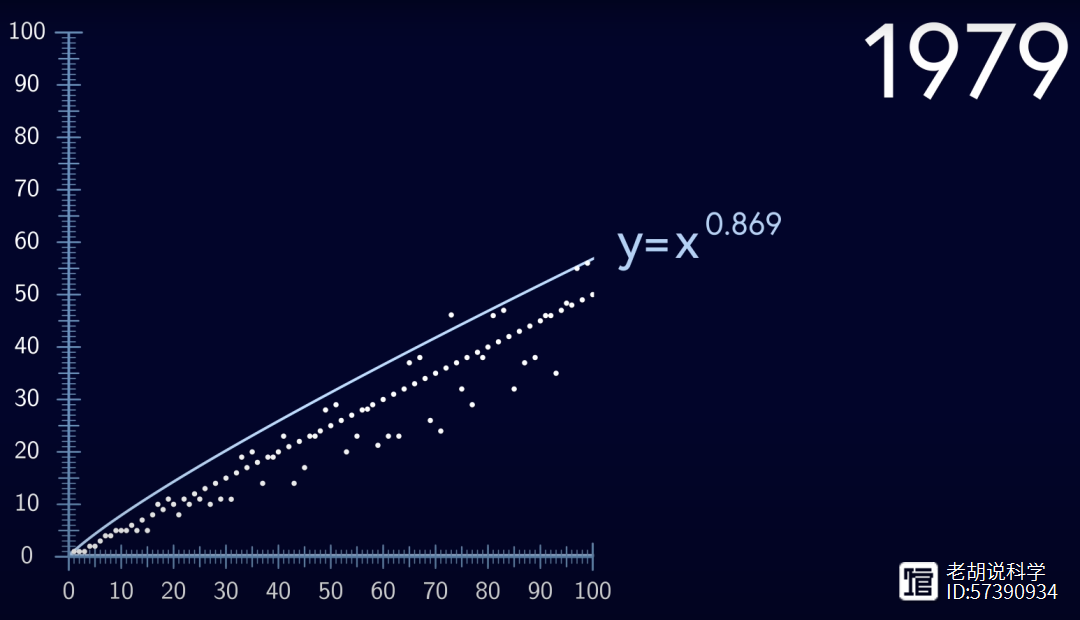
然后在1994年,它进一步降低到小于x的0.7925次方。
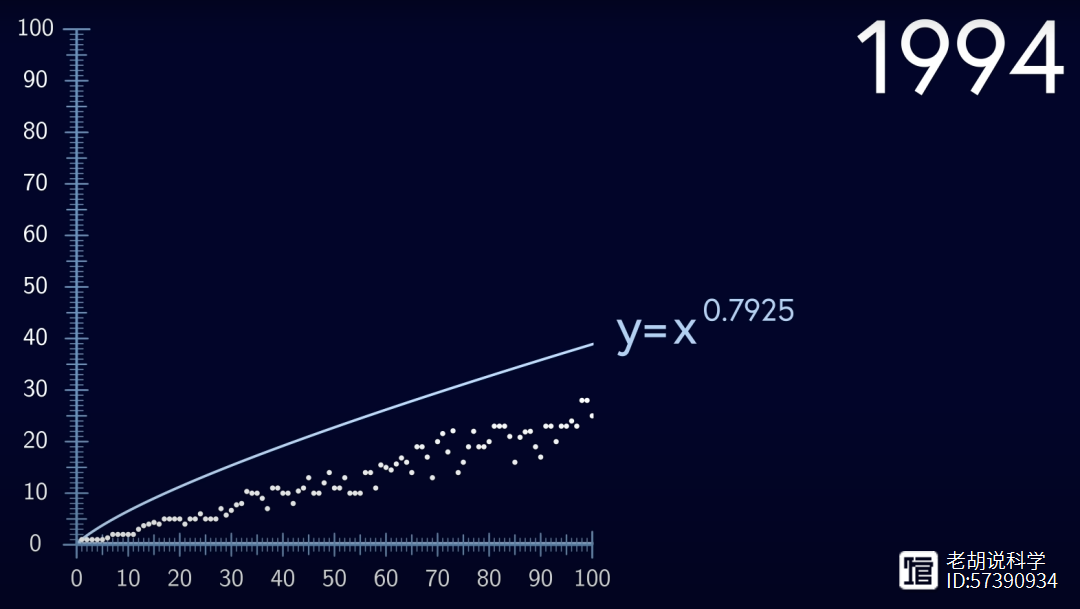
在这种情况下,“几乎所有数字”具有技术性的数学定义,意味着当你观察的数字趋向无穷大时,落在曲线下的数字比例趋向于1。
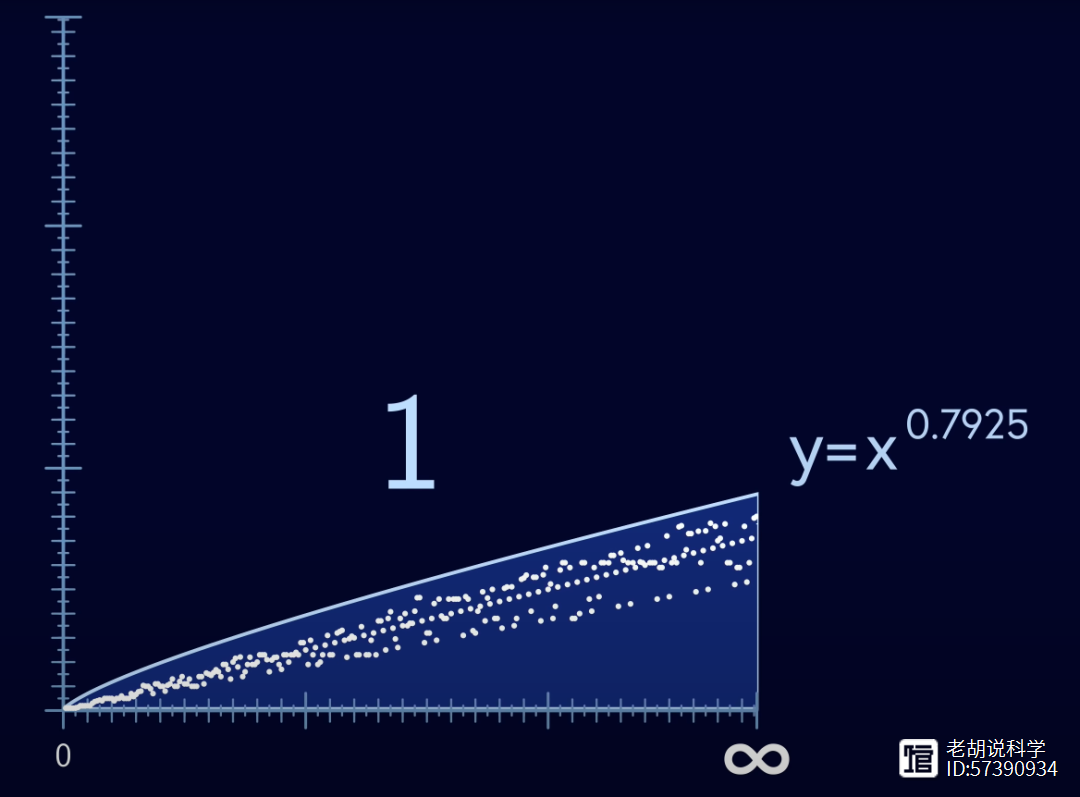
然后在2019年,世界上最伟大的在世数学家之一,陶哲轩,证明了3x 1遵循更严格的标准。

他证明了几乎所有的数字最终都会小于任意函数f(x),只要该函数在x趋向无穷大时也趋向无穷大。
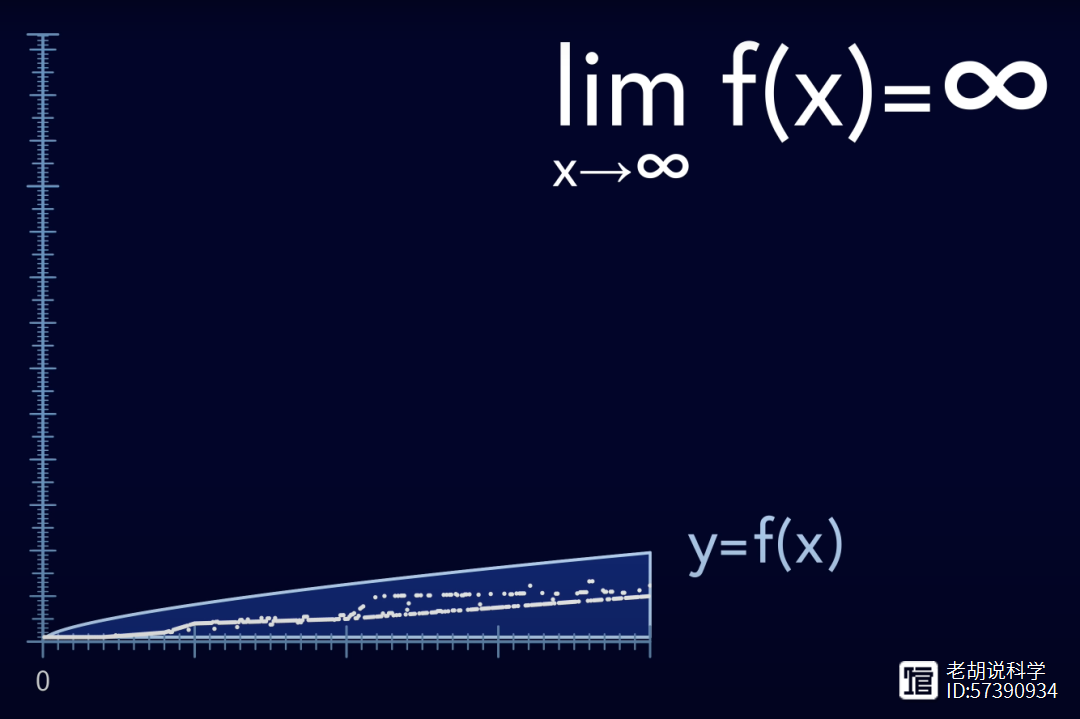
但是这个函数可以增长得非常慢,例如log x或者log log x,甚至是log log log log x。
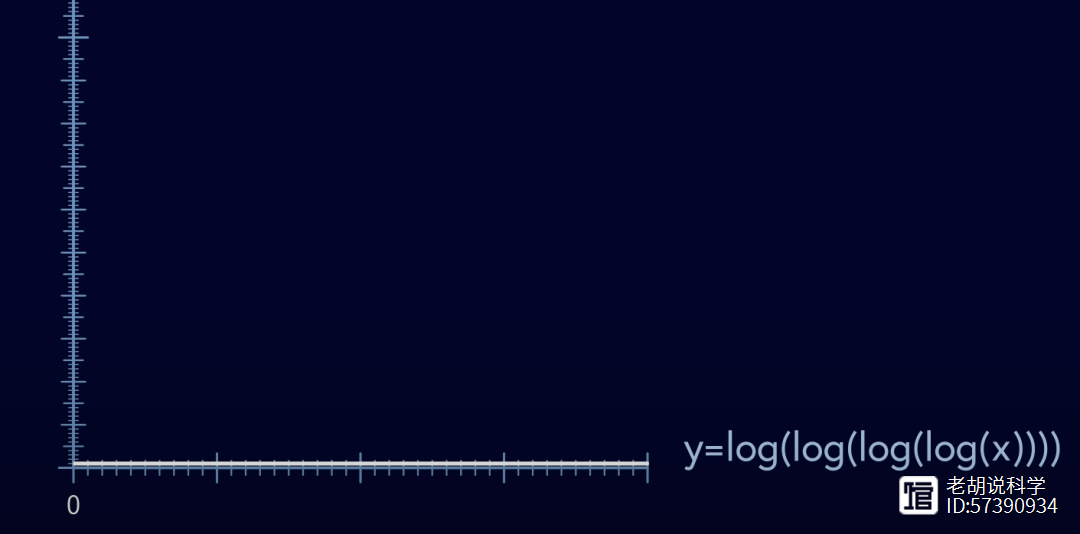
这意味着对于几乎所有的数字,可以保证在其序列中有一个任意小的数字。在2020年的一次公开演讲中,陶哲轩说这已经非常接近Collatz猜想了。
然而,迄今为止,还没有人证明为什么一个数字不能一直飙升到无穷大。而且,只需要一个这样的数字就足以证明猜想是错误的。或者,某些数字集合可能是一个与主图不相连的闭环。据我们所知,只有一个循环,即4-2-1。但是,如果包含负数,情况就变得奇怪了。在同样应用3x 1规则的情况下,不仅有一个循环,而且有三个独立的数字循环,它们从较低的数值,如-17和-5开始。

为什么在数轴的负数部分会出现不相连的循环,而在正数部分则没有呢?
现在,支持猜想的最有力的证据之一是陶哲轩证明几乎所有的数字序列中都有一个任意小的数字。但是,证明几乎所有数字都符合这一标准,并不等于证明所有数字都符合这一标准。在1到100之间有多少个完全平方数?答案是10个。

所以,在100以内的数字中,有10%是完全平方数。在1到1000之间有多少个完全平方数?答案是31个。因此,在1000以内的数字中,只有3.1%是完全平方数。数字越大,这个百分比就越小,以至于在极限情况下,你可以说几乎所有的数字都不是完全平方数。当x趋向无穷大时,不是完全平方数的数字比例趋向于1。
然而,我们知道有无穷多的完全平方数,并且我们知道它们分布在哪里。现在我们已经通过暴力方法测试了所有高达2的68次方的数字,并且它们都符合科拉茨猜想。但在所有数字的范围内,2的68次方几乎算不了什么。1919年乔治·波利亚提出的波利亚猜想(Polya conjecture)认为,对于任何给定的自然数,大多数自然数具有奇数个质因数。
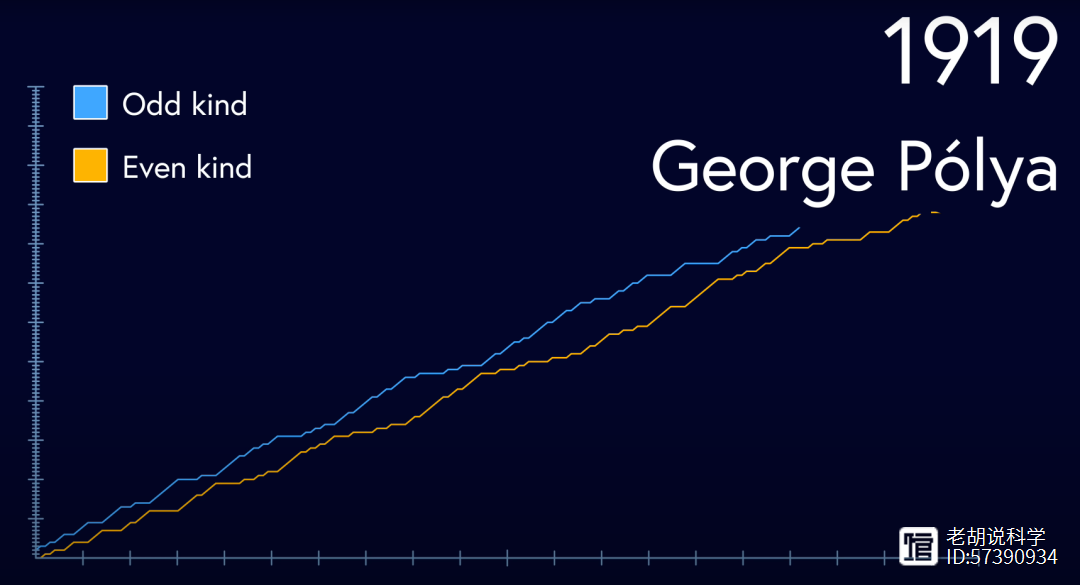
这个猜想最终在1958年被C·布赖恩·哈塞尔格罗夫证明是错误的,当时他找到了一个反例。这个反例的值是
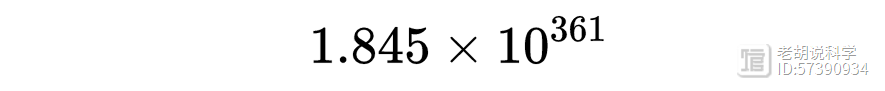
这个数字比已经检验过的3x 1的最大数字大约10的340次方。这意味着,即使我们已经测试了高达2的68次方的所有数字,也不能保证这个猜想是正确的,因为在所有数字的范围内,这个数字几乎微不足道。
我们需要继续探索和证明,寻找潜在的反例或者最终证明科拉茨猜想的正确性。然而,直到目前为止,这个猜想仍然是一个未解之谜。我们可以把3x 1看作是在图灵机上运行的一个简单程序,种子数是输入到这台机器的数据。

在这个例子中,2的68次方仅仅是一条68个方格长的输入带。你可以把它们想象成一串0和1,或者黑白方格。

这台机器已经把所有输入转换到这个68格方格带上,并将其降到1,但这说明不了什么。实际上,只要有限,计算一个表现出任意行为的数字是相当简单的。但在如果超出了你指定的有限部分之后,你就没有更多的控制权了。如果存在一个反例,那么有人猜到它的可能性几乎是0,因为所有可能性的空间太大,无法通过暴力搜索来穷举。2的1000次方不是一个可以搜索的空间。所以,如果我们要找到它,我们必须通过一种智能过程来找到它,而不是通过猜测和检验。
当然还有另一个可能性,那就是我们永远无法得知这个问题是无法决定的。

1987年,约翰·康威创建了3x 1的推广,这是一个他称之为Fractran的数学机器。他证明了这台机器是图灵完备的,这意味着它可以做任何现代计算机能做的事情。但这也意味着它受到停机问题的影响,即机器永远不会停止运行,因此不会给出输出。
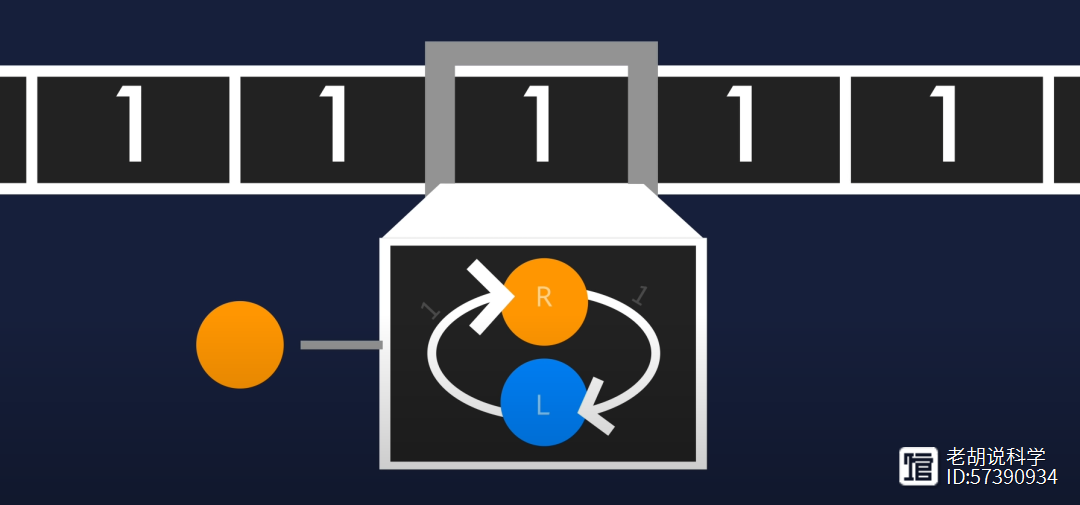
这并不能证明3x 1也受到停机问题的影响,但根据我们所知,我们可能永远无法证明科拉茨猜想是正确的还是错误的。
我一直认为数字是非常规整的东西,充满了模式、对称和重复。但现在我才意识到数字其实是多么奇特。最明显的例子是科拉茨猜想的Choral表示法,通过一个简单的数学运算产生了如此复杂、有机且难以捉摸的东西。

所有的数字是否都与这个结构相连?还是有一些独特的数字与这一切无关,或者延伸到无穷远?为什么这么难以分辨?
我想这就是为什么保罗·埃尔德什说,对于这样的问题,数学还不够成熟。我喜欢3x 1问题,因为它是一个几乎所有人都可以理解和研究的问题。实际上,自己尝试去解决问题是学习的最好方法。
- 0000
- 0001
- 0001
- 0002
- 0001















