有趣的生日悖论 揭秘23人中两位一天生日机率超50%

导语：世界上很多事情并不是非黑即白的，有很多东西不能细推，推敲出来就会出现矛盾，也就是大家常说的悖论。有关悖论的问题还有很多，有些人也疑惑龟兔赛跑是悖论吗，还有神奇的费米悖论等等，下面探秘志小编为大家介绍另外一种神奇的悖论-生日悖论，下面一起了解一下吧。

生日悖论

这个就是指一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%。也就意味着一个30人的小学班级中，两人生日一致的可能性更高。假如人数是30的几倍的话，这个概率更是会大于99%。

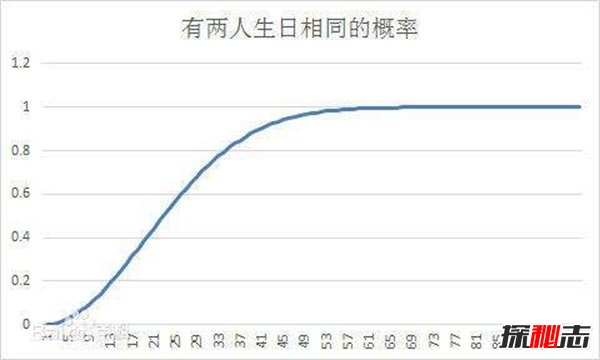
虽然从引起逻辑矛盾方面来看，似乎这个并不算是一种悖论，只有从这个数学事实与一般直觉相抵触的意义上，它才称得上是一个悖论。

悖论内容

如果一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中，存在两人生日相同的可能性更高。对于60或者更多的人，这种概率要大于99%。

不计特殊的年月，如闰二月。

先计算房间里所有人的生日都不相同的概率，那么

第一个人的生日是 365选365

第二个人的生日是 365选364

第三个人的生日是 365选363

:

:

:

第n个人的生日是 365选365-(n-1)

所以所有人生日都不相同的概率是：

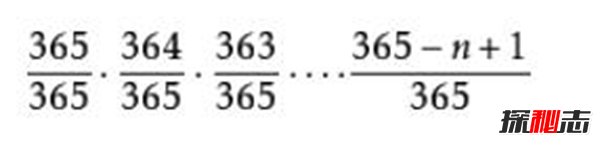
那么，n个人中有至少两个人生日相同的概率就是：

所以当n=23的时候，概率为0.507

当n=100的时候，概率为0.999999692751072

对于已经确定的个人，生日不同的概率会发生变化。下面用随机变量计算：

令X[i,j]表示第i个人和第j个人生日不同的概率，则易知任意X[i,j]=364/365

令事件A表示n个人的生日都不相同

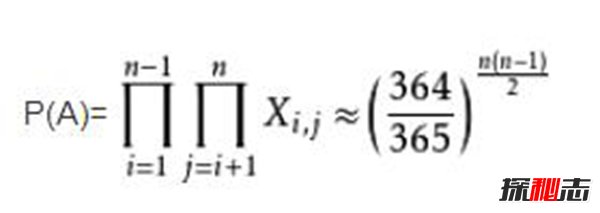
解P(A)<1/2，由对数可得：n>=23

相比之下，随机变量也同样的简单易懂而且计算起来要方便得多

理解悖论

这个问题的关键在于认识到相同生日的搭配可以是相当多的。比如23个人可以产生23 × 22/2 = 253种不同的搭配，而这每一种搭配都有成功相等的可能。从这样的角度看，在253种搭配中产生一对成功的配对也并不是那样的不可思议。

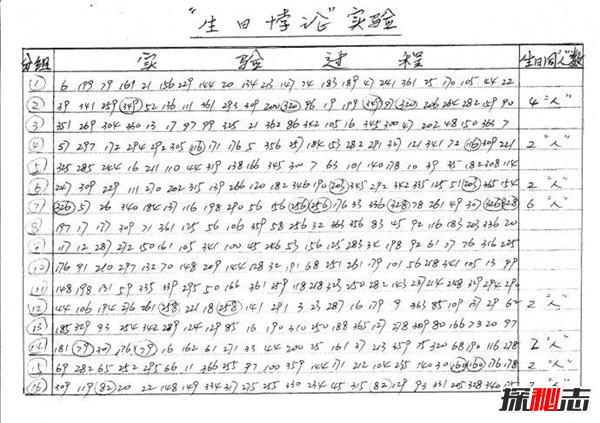
换一个角度，如果你进入了一个有着22个人的房间，房间里的人中会和你有相同生日的概率便不是50%了，而是变得非常低。原因是这时候只能产生22种不同的搭配。生日问题实际上是在问任何23个人中会有两人生日相同的概率是多少。

结语：看了这个生日悖论问题，大家是不是觉得和世界十大著名悖论一样也相当有意思。有些人认为这个悖论不能应用在生活中，实际上并不是这样，生活中很多东西都运用了这个有关悖论。